Search Results for: linear algebra

2022 — Year in Review

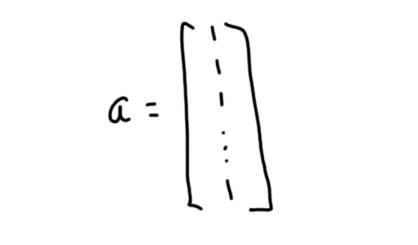
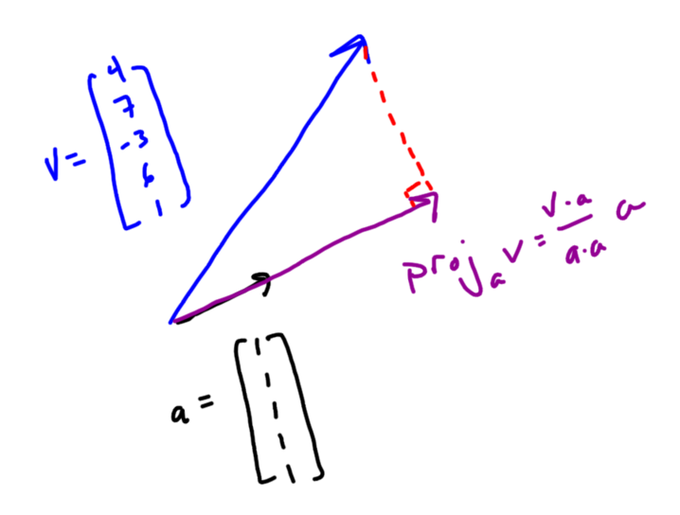
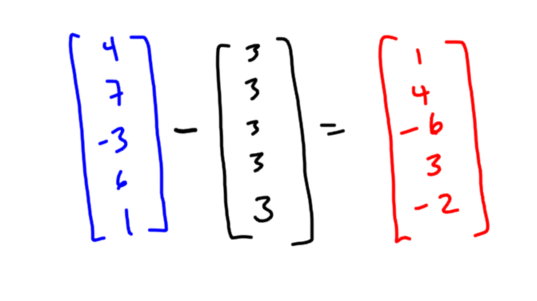
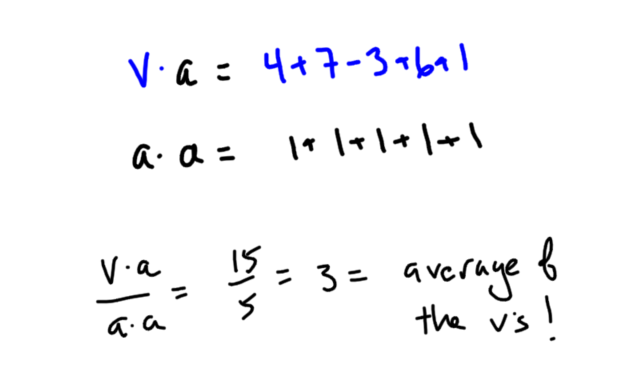In keeping up with (what is now a 10-year!) tradition, here’s a brief review of my professional year.

Without question my biggest professional accomplishment of 2022 was the publication of my book, Painless Statistics. People are buying it and even saying nice things about it! From start to finish it was an incredible learning process, and I now know what is meant by the saying “It is better to have written a book than to write one.”

I was happy to resume giving talks and workshop again in person in 2022. In the spring I returned to Queen’s College to speak to soon-to-be math teachers about making math by design. And after two years of remote-only teacher workshops, I was thrilled to return to the Math for America offices for The Geometry of Linear Algebra. It’s been exciting to learn so much linear algebra as I teach it, and I already have new workshops and talks scheduled for 2023.

On top of publishing Painless Statistics, it was another busy year of writing. As usual my column for Quanta Magazine provided a year full of the best kind of mathematical challenges, and I had a blast writing about brownie bake-offs and geometric dissections, different kinds of infinities, and Wordle, among other things. And I reviewed Ben Orlin’s book Math Games with Bad Drawings for the American Mathematical Monthly.

Above all, it was just nice to have a professional year that seemed to be trending toward normal.

Here’s to an even more normal 2023!

Related Posts

By MrHonner, ago

The All 1s Vector

Here’s a short post based on a Twitter thread I wrote about a very underappreciated vector: The all 1s vector!

Image

Every vector whose components are all equal is a scalar multiple of the all 1’s vector. These vectors form a “subspace”, and the all 1’s vector is the “basis” vector.

Let’s say you have a list of data — like 4, 7, -3, 6, and 1 — and you put that data in a vector v. An important question turns out to be “What vector with equal components is most like my vector v?”

To answer that question you can *project* your vector onto the all 1’s vector. You can think of this geometrically — it’s kind of like the shadow your vector casts on the all 1’s vector. There’s also a formula for it that uses dot products.

Image

Because of the way the dot product works and the special nature of the all 1’s vector, v•a is the sum of the elements of v and a•a is the number of elements in v. This makes (v•a)/(a•a) the mean of the data in v!

Image

Since 3 is the mean of your data, the vector with equal components that is most like your vector is the all 3’s vector. This makes sense, since if you’re going to replace your list of data with a single number, you’d probably choose the mean.

Now the cool part. Look at the difference in these two vectors: These are the individual deviations from mean for each of your data points, in vector form!

Image

And geometrically this vector of deviations is perpendicular to the all 1’s vector! You can check this using the dot product.

Image

So data can be decomposed into two vector pieces: one parallel to the all 1’s vector with the mean in every component, and one perpendicular to that with all the deviations. You can see hints of independence, variation, standard deviation lurking in this decomposition.

You can check out the original thread on Twitter here, including some very interesting replies!

Related Posts

By MrHonner, ago

2021 — Year in Review

A return to in-person schooling was the biggest news of 2021. I don’t want to be accused of burying the lede.

It’s been great to be back. It’s also been an interesting challenge trying to weave together what I learned over the past year-and-a-half as a full-time remote teacher with what I was doing in-person before that. Add in new colleagues, redefined priorities for teacher teams, and a brand new course to teach and it’s been a pleasantly busy return to the building.

I’ve also stayed busy with a variety of talks and webinars this past year. As always I ran several workshops for Math for America, like Bringing Modern Math into the Classroom in January and It’s All Linear Algebra in November. This summer I participated in a roundtable discussion at the National Museum of Mathematics on math education. And I was thrilled and honored to run a week of morning math for the Park City Math Institute’s Teacher Leadership Program, satisfying two long-standing professional goals: to participate in PCMI and to finally make sense of complex multiplication!

I continued to write my column for Quanta Magazine, which is on ongoing professional highlight. The year started with the crooked geometry of round trips (an article that was picked up by Wired magazine) and covered everything from hot dogs to goats to tricky job interview questions.

I was proud to keep up my Remote Learning Journal throughout the 2020-21 school year, and was happy to have the opportunity to reflect on the totality of my experience on the MAA’s Math Values blog, where I published “Let’s Remember the Year Everyone Wants to Forget“. I was also able to capture some fun moments in writing this past year, with a short story about an absolutely brilliant student solution to a calculus problem as well as a Seussian poem proof of the irrationality of the square root of 2.

Without question my single biggest professional project this year, writing or otherwise, was getting a manuscript submitted. I knew it would be more work than I expected, and it was. But the process was exciting and eye-opening and worthwhile, and I am thrilled that Barron’s Painless Statistics will be out in June 2022.

It’s been another year full of challenges, changes, and opportunities, and I hope 2022 brings us a healthier balance of all those things.

Related Posts

By MrHonner, ago

SIAM ED16

siam-ed16I’m excited to be heading to Philadelphia this weekend for the SIAM Conference on Applied Mathematics Education (SIAM ED16).

I’ll be presenting on the work I do with mathematical simulation in Scratch, and I’m really looking forward to the variety of talks on bringing applied mathematics and computing into classrooms.  In particular, I’m excited to hear Maria Hernandez from NCSSM talk about how to teach modeling and Gil Strang from MIT talk about the teaching of Linear Algebra.

You can learn more at the conference website, and see the full conference schedule here.

Related Posts

 

By MrHonner, ago

Math Photo: Change of Coordinates

Change of Coordinates

Shining through the rectangular grid of chain links, the sun creates a second, compressed coordinate system in shadow.  This reminds me of changing coordinate systems, as in linear algebra or a u-du substitution .

Often, a new coordinate system can provide a cleaner environment for solving a problem.  And as long as we understand the transformation that got us there, we can usually take our solution back with us when we return.

By MrHonner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: