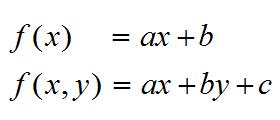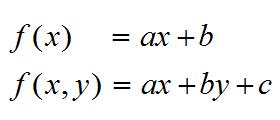Arguments that suggest we over-emphasize mathematics in education don’t bother me. I love math and see its utility in every aspect of my life, but I understand not everyone feels this way. Also, when someone says we shouldn’t teach math, or we should teach less, it encourages me to reflect on my own beliefs about math and teaching. This is usually a valuable experience.
So I read “Is Algebra Necessary?“, Andrew Hacker’s OpEd in the New York Times, knowing that I probably wouldn’t agree with much of it, but still prepared to examine my beliefs. Hacker offers up a few of the standard reasons why students shouldn’t be forced to take “Algebra” in high school (“it’s too hard”; “it turns kids off”; “not everyone’s going to be an engineer”), but he doesn’t really bring anything new or substantial to the discussion.
One thing I did find interesting, however, was Hacker’s suggested fix: instead of “Algebra”, we should be teaching courses like “Citizen Statistics”.
It could, for example, teach students how the Consumer Price Index is computed, what is included and how each item in the index is weighted — and include discussion about which items should be included and what weights they should be given.
This is indeed a good idea. Ironically, exploring the mathematics of the CPI is largely an algebraic activity.
Discussing which items should be included means creating a mathematical model and declaring variables for the unknown quantities we wish to investigate. These fundamental skills are taught and emphasized in high school algebra.
Determining the weights that these items should be given essentially amounts to finding the coefficients of some function of those variables and exploring the consequences of those choices. In their basic forms, these skills are also taught and developed in high school algebra.
Thus, it seems to me that Hacker is suggesting we replace Algebra, with, well, Algebra.
There are worthwhile discussions to be had about what we are teaching, why we are teaching, and how we are teaching. But those discussions should be led by people who really understand what’s going on. If Andrew Hacker thinks we should replace Algebra with Algebra, then someone else should be leading the discussion.
Related Posts
