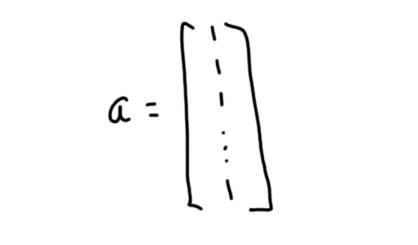
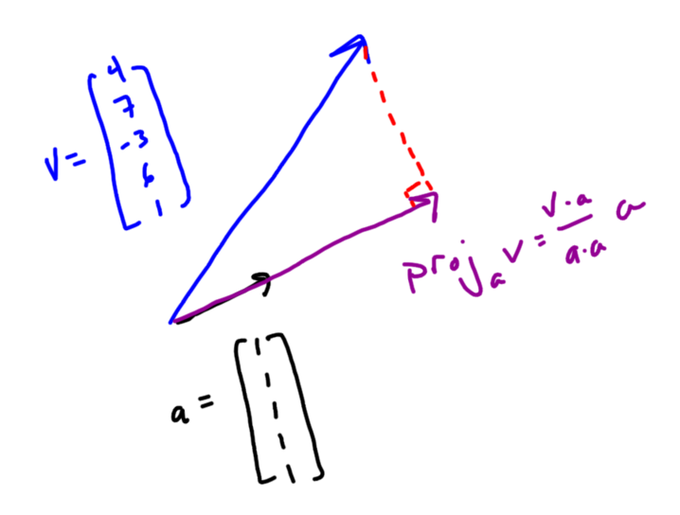
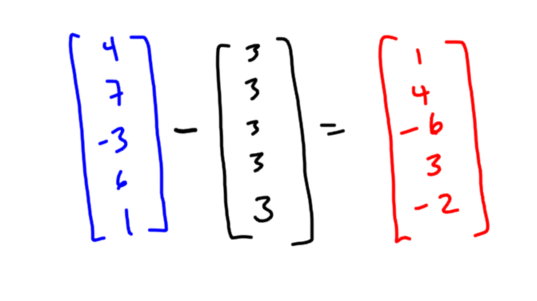
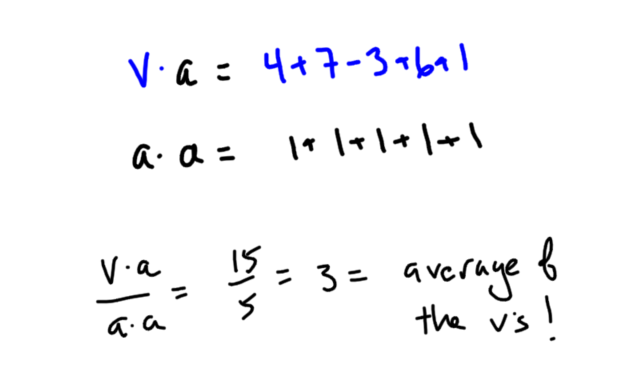I am thrilled to announce the release of my new book, Painless Statistics!
Painless Statistics, an entry in the Barron’s Painless series, is written to serve as both a supplementary resource for students taking statistics in school as well as a stand-alone resource for adults who are learning (or re-learning) stats on their own.
Painless Statistics begins with an example of working with data, and covers everything from summary statistics and representations of data to sampling distributions and statistical inference. The book also includes plenty of problems that get you thinking about and applying the important ideas in each chapter.
My hope is that Painless Statistics can be a useful resource for middle school, high school, and even college students learning statistics, as well as for lifelong learners interested in understanding the fundamental mathematical ideas at the intersection of statistics, probability, and inference.
I also think the book would be a great resource for any math teacher who might not see themselves as a statistics teacher but would like to better understand the fundamental ideas in statistics. If by reading Painless Statistics you learn 10% of what I learned by writing it, I think you’ll find it a worthwhile purchase.
If you or someone you know is learning statistics, or would like to learn statistics, please consider picking up a copy of Painless Statistics! It will be available in bookstores everywhere starting June 7th, and you can also order it online. I’ve included the Table of Contents below, and you can take a look inside at the first chapter here.
Painless Statistics Table of Contents
Chapter One: An Introduction to Data
Chapter Two: Data and Representations
Chapter Three: Descriptive Statistics
Chapter Four: Distributions of Data
Chapter Five: The Normal Distribution
Chapter Six: The Fundamentals of Probability
Chapter Seven: Conditional Probability
Chapter Eight: Statistical Sampling
Chapter Nine: Confidence Intervals
Chapter Ten: Statistical Significance
Chapter Eleven: Bivariate Statistics
Chapter Twelve: Statistical Literacy