Since the advent of the “Common Core” Regents exams in New York state, there has been a noticeable increase in decidedly Pre-Calculus content on the tests. Questions involving rates of change, piecewise functions, and relative extrema now routinely appear on the Algebra I and Algebra II exams. Unfortunately, these questions also routinely demonstrate a disturbing lack of content knowledge on the part of the exam creators.
Here’s number 36 from the January, 2018 Common Core Algebra I Regents exam.
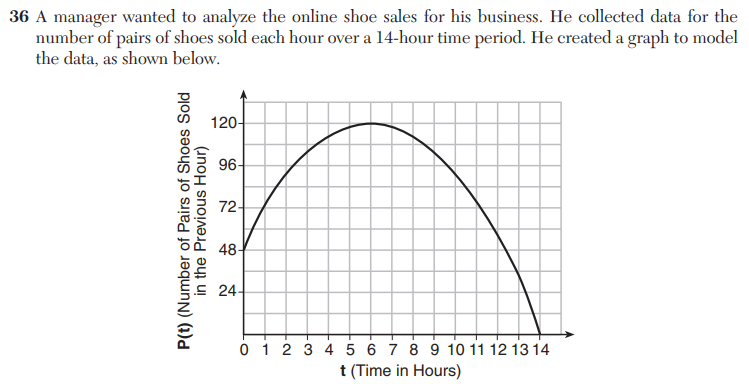
This graph represents “the number of pairs of shoes sold each hour over a 14-hour time period” by an online shoe vendor. A simple enough start. But things start to get tricky halfway down the page, when the following directive is issued.
State the entire interval for which the number of shoes sold is increasing.
The answer must be 0 < t < 6, because that’s when the graph is increasing, right? The official rubric says so, and the Model Response Set backs it up (this Model Response has been edited to show only the portion currently under discussion).

But 0 < t < 6 is not the correct answer. Can you spot the wrinkle here? Basically, the number of shoes sold is always increasing.
The graph shown is a model of the number of shoes sold per hour. The model shows that, at any time between t = 0 and t = 14, a positive number of shoes are being sold per hour. In short, more shoes are always being sold. That means the number of shoes sold is always increasing. The correct answer is 0 < t < 14.
The exam creators have made a conceptual error familiar to any Calculus teacher: they are conflating a function and its rate of change.
In this problem, the directive pertains to the number of shoes sold. But the given graph shows the rate of change of the number of shoes sold. The given graph is indeed increasing for 0 < t < 6, but the question isn’t “When is the rate of change of shoes sold increasing?” The question is “When is the number of shoes sold increasing?” Since a function is increasing when its rate of change is positive, this means the number of shoes sold is increasing whenever the graph is positive. Thus, the answer is 0 < t < 14.
After the exam was given and graded, those in charge of the Regents exams became aware of the error. They quickly issued a correction, updated the rubric, and instructed schools to re-score the question (giving full credit for either 0 < t < 6 or 0 < t < 14). Thankfully, it didn’t take a change.org campaign and national media attention for them to admit their error.
But as usual, they did their best to dodge responsibility.
In their official correction, the exam creators blamed the issue on imprecision in wording, pretending that this was just a misunderstanding, rather than an embarrassing mathematical error. This is something they’ve done over and over and over again. These aren’t typos, miscommunications, or inconsistencies in notation. These are serious, avoidable mathematical errors that call into question the validity of the very process by which these exams are constructed, graded, and, ultimately, used. We all deserve better.
Related Posts