Regents Recap — January, 2018: Problems with Pre-Calculus
Since the advent of the “Common Core” Regents exams in New York state, there has been a noticeable increase in decidedly Pre-Calculus content on the tests. Questions involving rates of change, piecewise functions, and relative extrema now routinely appear on the Algebra I and Algebra II exams. Unfortunately, these questions also routinely demonstrate a disturbing lack of content knowledge on the part of the exam creators.
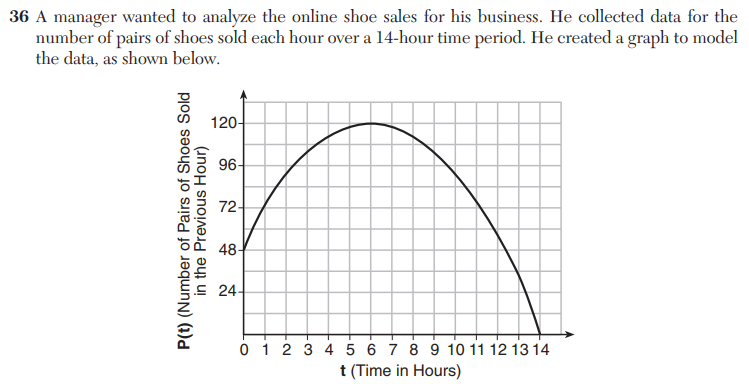
Here’s number 36 from the January, 2018 Common Core Algebra I Regents exam.
This graph represents “the number of pairs of shoes sold each hour over a 14-hour time period” by an online shoe vendor. A simple enough start. But things start to get tricky halfway down the page, when the following directive is issued.
State the entire interval for which the number of shoes sold is increasing.
The answer must be 0 < t < 6, because that’s when the graph is increasing, right? The official rubric says so, and the Model Response Set backs it up (this Model Response has been edited to show only the portion currently under discussion).
But 0 < t < 6 is not the correct answer. Can you spot the wrinkle here? Basically, the number of shoes sold is always increasing.
The graph shown is a model of the number of shoes sold per hour. The model shows that, at any time between t = 0 and t = 14, a positive number of shoes are being sold per hour. In short, more shoes are always being sold. That means the number of shoes sold is always increasing. The correct answer is 0 < t < 14.
The exam creators have made a conceptual error familiar to any Calculus teacher: they are conflating a function and its rate of change.
In this problem, the directive pertains to the number of shoes sold. But the given graph shows the rate of change of the number of shoes sold. The given graph is indeed increasing for 0 < t < 6, but the question isn’t “When is the rate of change of shoes sold increasing?” The question is “When is the number of shoes sold increasing?” Since a function is increasing when its rate of change is positive, this means the number of shoes sold is increasing whenever the graph is positive. Thus, the answer is 0 < t < 14.
After the exam was given and graded, those in charge of the Regents exams became aware of the error. They quickly issued a correction, updated the rubric, and instructed schools to re-score the question (giving full credit for either 0 < t < 6 or 0 < t < 14). Thankfully, it didn’t take a change.org campaign and national media attention for them to admit their error.
But as usual, they did their best to dodge responsibility.
In their official correction, the exam creators blamed the issue on imprecision in wording, pretending that this was just a misunderstanding, rather than an embarrassing mathematical error. This is something they’ve done over and over and over again. These aren’t typos, miscommunications, or inconsistencies in notation. These are serious, avoidable mathematical errors that call into question the validity of the very process by which these exams are constructed, graded, and, ultimately, used. We all deserve better.
Related Posts
- Regents Recaps
- The Worst Regents Question of All Time
- The Underlying Problem with the New York State Regents Exams
- Promoting Bad Habits

9 Comments
Evelyn Lamb · March 6, 2018 at 6:52 pm
I really don’t like the fact that it’s not a bar graph! (Or some other chart that more accurately reflects that this is a discrete process.) Maybe the question should have asked the student to critique the manager’s choice of data visualization.
MrHonner · March 7, 2018 at 8:21 am
It’s funny that you point out the discrete nature of this process. Here’s the first part of this problem:
The manager believes the set of integers would be the most appropriate domain for this model. Explain why he is incorrect.
The “complete and correct” answer, according to the state, is that “The manager is incorrect because time can be fractions and decimals.”
It seems to me that the integers are precisely the appropriate domain for this model (for several reasons). And it sounds like you might agree! I didn’t even bother mentioning it, as I was already growing tired of the writing about the first error.
Evelyn Lamb · March 7, 2018 at 10:09 am
That is really unfortunate! I mean, I guess I can sympathize with deciding to make time continuous, but if we do that, we need to think about what kinds of graph make sense with one variable being continuous and one being discrete! The graph has to be a stairstep function in that case, not a smooth curve. Wouldn’t it be nice to encourage students to think critically about how we might best represent the data for this manager’s purposes?
Gabe Rosenberg · March 7, 2018 at 8:19 pm
I disagree that it HAS to be stairstep. Presumably for each hour there is a data point for that hour. The manager then decided to choose a quadratic curve to try to fit the data. That is a reasonable choice. Interpolation here seems reasonable. One could have an interesting classroom discussion over whether to choose to model the domain discretely or continuously. This is a great example where there are pros and cons and no one “right” answer. The problem is trying to make it a standardized test question where a reasonable justifiable answer gets less or no credit.
Alax · March 7, 2018 at 8:19 pm
I call shenanigans on the test creators’ logic and inconsistency.
The text says one thing about the dependent variable, “the number of pairs of shoes sold each hour over a 14-hour time period”; the graph another, “Number of pairs of shoes sold in the previous hour”.
Both are discrete.
(A) implies a horizontal segment for some value during the 60 minutes previous to each recorded moment until another pair of shoes is sold, counting some sales many times.
(B) implies that the mark for all of the time between 2:00 and 3:00 is the single number representing rate of shoes from 1:00:00 to 1:59:59.99999999999
Joel David Hamkins · March 7, 2018 at 8:26 pm
What about the issue that the student in the response rubric referred to x, rather than t? I would find that to fall short of “complete and correct”, since it is often an important mathematical point to keep straight which variable refers to which quantity, and in the set up here, there is no meaning for x.
MrHonner · March 7, 2018 at 8:56 pm
I agree that it is a serious problem in the student’s response that needs to be addressed. As a teacher I am always emphasizing precision (in argument, language, notation) and I would (and do!) make a big deal about this.
But it’s a tough call about how to handle this on this exam. The response in question is worth one points. Marking it wrong because the student wrote ‘x’ instead of ‘t’ would be a 100% deduction. That seems harsh.
Donny Brusca · January 9, 2019 at 6:43 am
Mr. Honner,
I’m curious, have you heard any complaints about the incorrect grading of question #29 of the August 2018 Geometry Regents? There’s nothing inherently wrong with the question, but the Model Responses give full credit for answers that are clearly invalid.
Nowhere in the description does it state that the pole is perpendicular to the ground. Yes, it “looks” perpendicular in the diagram, but there is nothing that supports this assertion. (Haven’t we all seen slanted telephone poles in our neighborhood?) Nevertheless, the Model Responses award full credit to students who state that the angles at the bases of the two poles are congruent because they are both right angles.
Instead, a correct response should state that these angles are congruent since they are corresponding angles formed by parallel lines cut by a transversal. (Or, it could use the same reason for the angles formed by the intersections of the poles with the support wire.)
Are we now teaching students to assume an angle is a right angle because it looks like one in a diagram??
Donny Brusca
MrHonner · January 11, 2019 at 4:44 pm
Donny-
I did not notice that, nor did I hear anyone complaining about it until you brought it to my attention. Definitely sounds like something that would be a good fit for my talk on the problems with mathematical modeling in Regents exam questions!