Regents Recap — January 2015: It’s True Because It’s True
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
This is question 25 from the Common Core Algebra exam.
I’ve already complained about the contrived, artificial contexts for these questions (why not just ask “Is the sum of these two numbers rational or irrational?”), so I’ll ignore that for now. What’s worth discussing here is the following sample student response provided by the state.
So, why is the sum of a rational number and an irrational number irrational? Because the sum of a rational number and an irrational number is always irrational. This circular argument is offered as an example of a complete and correct response.
I’m not sure there’s a way to rewrite this question so that it admits a sensible answer. That’s probably a good indication that it shouldn’t be on a high-stakes test.
As I’ve argued time and again, questions on these exams should stand as examples of proper mathematics. But questions like this actually encourage bad habits in students, and teachers too, who are being told that this constitutes an appropriate response to this question. This is yet another example of the danger of simply tacking on “Justify your reasoning” to a high-stakes exam question.
Related Posts
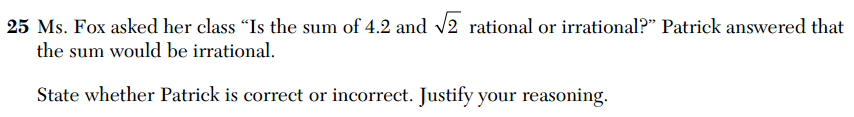

6 Comments
Kenneth Tilton · March 17, 2015 at 9:23 am
Whoa, I did not realize how bad are these tests and their scoring. I’ll go read that other post on the contrived questions.
If the tests really are this bad, I suggest we implement an evaluation scheme for the tests and close any testing company that comes up short. That will make the tests better. Kidding.
Meanwhile, is anyone anywhere challenging the unexamined presupposition that being good at X means being able to explain X? One reason I do not read the comments of computer programmers on the algorithm they are explaining is that they cannot write to save their lives.
The idea behind requiring the justification is to expose superficial mechanical aptitude (they remembered what FOIL means but do not understand that they are applying the distributive property twice). Fine. But is it possible they get that but are weak at expository writing? Or at the kind of writing this examiner can follow?
Worse, what if they are left-brained non-verbal? They see the motivating demonstration once, absorb it, and just plain get it? Do we still want to score them on being able to supply a proof?
Bowen Kerins · March 17, 2015 at 9:48 am
WHAT IS THIS I DON’T EVEN
I agree with the comment that there’s not much rewriting possible here to make the problem allow a better justification than this. Perhaps a better question would be multiple choice, with some options where one of them multiplies to an irrational? The PARCC and SBAC items equivalent to this are usually a “multiple sort” since a four-choice multiple choice comes down to picking the one that is unlike the others.
Hao Ye · March 17, 2015 at 3:38 pm
I don’t think it’s necessarily a bad justification to use the principle that the sum of a rational number and an irrational number is irrational. For a complete answer, the student must do 3 things:
(1) acknowledge that 4.2 is rational
(2) acknowledge that sqrt(2) is irrational
(3) remember and apply the above principle.
It seems straightforward to me to apply a simple proof-by-contradiction, but that seems like it would be beyond the scope of a common core Algebra test.
The pseudo-context is rather absurd, though.
Kenneth Tilton · March 17, 2015 at 3:59 pm
I think you are right that a proof-by-contradiction is asking too much, but you might agree that “because it always is” is an unacceptable answer. It suggests that it is by definition or that we have checked all the irrationals. So this test has backed itself into a corner where it has to give credit for an incorrect justification.
The question should have either not demanded a justification or should not have been on the exam. Sadly, my guess is “Justify your reasoning” got tossed in because that is what these “superior” tests ask.
MrHonner · March 17, 2015 at 7:34 pm
The student certainly has no better alternative than to say than what has been said. I suspect the vast majority of high school students have never been shown how to demonstrate that a number is irrational.
But that doesn’t validate this as appropriate justification. And I think it’s dangerous to tell students, and teachers, that this kind of circular reasoning constitutes valid mathematical justification.
Elizabeth Kamerer · March 17, 2015 at 8:30 pm
I am so glad to see there are other math teachers out there who are as annoyed by questions like this one as I. First of all, students aren’t supposed to just memorize in this new curriculum. The philosophy, which I agree with, is allegedly to teach them to mathematically reason. Well, I don’t believe there is any debate what so ever that this is a lame exercise to give students. If they explained that the square root of two is a decimal which goes on infinitely without a repeating string and that if you add 4.2 to this infinite decimal, the decimal is still infinite and still remains without a repeating pattern, I’d be in. This would then lead them to understanding ideas such as converging/diverging series and how we look at the end. Again, I thank all of you for echoing the lameness of this question.