Regents Recap — January 2018: How Do You Explain That 2 + 3 = 5?
This has quickly become my new least-favorite kind of Regents exam question. (This is number 32 from the January, 2018 Algebra 2 Regents exam.)
What can you say here, really? They’re equal because they’re the same number. Here’s a solid mathematical explanation. Right?
Wrong.
According to those who write the scoring guidelines for these exams, this is a justification, not an explanation. Because students were asked to explain, not justify, this earns only half credit.
This is absurd. First of all, this is a perfectly reasonable explanation of why these two numbers are equal. This logical string of equalities explains it all. This clear mathematical argument demonstrates what it means to raise something to the power 3/4.
Second, whatever it is that differentiates an “explanation” from a “justification” in the minds of Regents exams writers, it’s never been made clear to test-takers or the teachers who prepare them. A working theory among some teachers is that “explain” just means “use words”. Setting aside how ridiculous this is, if this is the standard to meet, students and teachers need to be aware of it. It needs to be clearly communicated in testing and curricular materials. It isn’t.
Third, take a look at what the the test-makers consider a “complete and correct response”.
In this full-credit response, the student demonstrates a shaky mathematical understanding of the situation (why are they using logarithms?) and writes a statement (“81 with four roots gives you 3”) that, while on the right track, is in need of substantial mathematical refinement. Declaring this to be a superior response to the valid mathematical argument above is an embarrassment.
These tests are at their worst when they encourage and propagate poor mathematical behavior. We deserve more from our high-stakes exams.
Related Posts
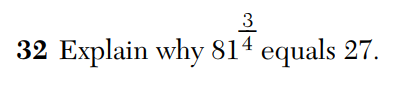
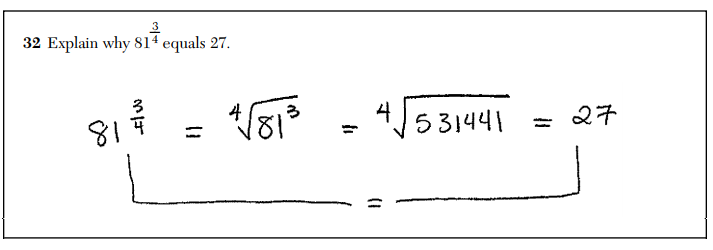


6 Comments
Donny Brusca · February 20, 2018 at 9:46 am
Well said! I completely agree.
I wonder, would this be a valid explanation? “When I enter 81 to the 3/4 power in my calculator, the answer is 27.”
MrHonner · February 20, 2018 at 1:33 pm
Good question, Donny. And one I probably don’t want to know the answer to.
Michael Paul Goldenberg · February 20, 2018 at 10:29 am
Having scored state math tests for one of the companies that contracts in Michigan to do such things (they aren’t the test publishers and they score for states outside of Michigan at the Michigan site where I worked several times), this is hardly an anomaly. Some committee writes a rubric for a test item which is passed along to scorers who receive training as a group on the way to score a given item before actual scoring is done. It really doesn’t matter what anyone raises during training that is critical of the rubric: its word is law and if a scorer wishes to keep working, it is imperative that s/he master the thinking of the rubric-writers, apply that thinking consistently, and get results that are in synch with how others are scoring. Too much variability will lead to issues for those out of step.
I would be rather unhappy with the above, though it would certainly help to see the rubric and more anchor papers used to illustrate its use. You haven’t “explained the thinking” of the rubric writers, but simply given an example. 🙂
That said, here’s the real scandal. From time to time while scoring a state test, we would be called together in our team and re-trained on an item we’d already been scoring. That is, something would come down from the state to the company and then to us through team or room leaders changing what was or was not to be given a certain score (it could be that on a 0, 1, 2 scale, some sort of answer would move up or down 1 point on the scale.
Fine and dandy, you might say. Good that the all-wise adjust their thinking. But here’s the rub. The first time this happened, I asked when we would go back over previously-scored papers to assign the proper credit. And as you might guess, given the time and cost issues for the state and the company, the answer was, “Never.” Imagine parental reaction to that if they knew.
MrHonner · February 20, 2018 at 1:40 pm
Michael-
The Regents rubrics themselves are vague to the point of uselessness. It’s these Model Responses, which are generated by the state DOE and distributed prior to scoring, which communicate all the nuance of how to grade each item. Thus, this isn’t a matter of teachers working with an inflexible rubric: for all intents and purposes, this is the rubric from the DOE.
And I have no doubt the corruption inside the private testing and scoring industry is obscene. As much as I complain about New York’s system, I am thankful they make they tests and supporting documentation transparent. It at least gives us the opportunity to bring these issues to light and have productive conversations about them.
Amy Hogan · February 20, 2018 at 10:30 am
To me, the clear award for absurdity goes to the question itself. But runner-up goes to the grading rubric for sure.
1. This question is unimaginative and lacks assessment intent. Because students can use their calculator to establish this equality, it’s not clear what mathematical understanding a problem like this could really give. Maybe test writers were hoping for a softball question on rational exponents, but something that exposes low-level comprehension of this topic is more suitable for a multiple choice question.
2. The idea that ‘explain’ dictates the use of words is also not clear and is not consistent across all math tests. Mathematical sentences are most certainly logically equivalent to words. If not, then every word problem ever should be banned from the math Regents.
3. The question is vague, leaving opportunities for more than one approach. And that makes for a free-for-all when it comes to grading. Especially with the completely unhelpful scoring rubric. You have now _guaranteed_ that this question will not be graded consistently across the state.
4. It has become clearer and clearer to me that the state is actually penalizing students who know and understand math by creating this type of rubric on the Regents. Why would the state want to create an exam question that can’t differentiate between a student who doesn’t understand the topic and one who doesn’t understand what the question is asking them to communicate?
MrHonner · February 20, 2018 at 1:46 pm
All good points, Amy. (Though I think you meant “inconsistently” in 3.)
As to (1), Donny raises an interesting point in a comment above: what if a student had written “I evaluated both of these on my calculator and they are the same.” Does that constitute explanation?
And as to (4), this was one of my tertiary concerns when I started analyzing these exams years ago. But like you, I am now starting to see this as a real problem: students who really know what they are doing are increasingly at risk of being penalized for not providing the kind of low-quality response these Regents exams often demand.