After developing a simple metric for evaluating the success of NBA draft selections, I used that metric to investigate talent dispersion in the draft and then to compare the strength of various “draft classes”. As a third application of this metric, I will now analyze the success each NBA teamin making their draft picks.
I am using the total number of minutes played in the first two years of a player’s career as the basic quantification of draft pick value (the reasoning for this is explained in detail in NBA Draft Math, Part I).
In order to rate the success of a team, I looked at how each team’s draft pick performed relative to the average player chosen at that draft position for the NBA drafts between 2000 and 2009. I then computed the percentage difference between that team’s choice and the average player at that pick. The team’s overall rating is then the average of the percent differences for every draft pick.
The chart below summarizes the analysis for the Philadelphia 76ers.
As you can see, all but one of the 76ers draft choices performed better than the average player selected at that draft position. Overall, draft picks selected by Philadelphia performed about 34% better than average; they topped the list in this ranking.
This chart displays all NBA teams whose picks performed better than average. In addition to the 76ers, teams that performed notably well by this measure were the San Antonio Spurs, the Houston Rockets, and (surprisingly?) the New York Knicks.
The teams that performed worst in the analysis were the Boston Celtics, the Portland Trailblazers, and the Charlotte Bobcats.
Some interesting results! The basic limitations of this metric have been addressed in NBA Draft Math, Part I, but this simple approach has opened up a lot of opportunities for analysis, and naturally, improvement.
Related Posts
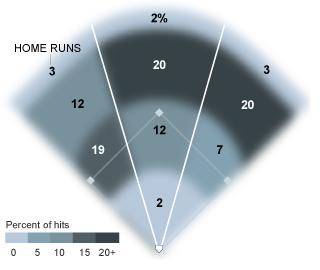In celebration of Derek Jeter’s 3,000th major league hit, the New York Times ran a really cool infographic displaying the relative frequencies of where those 3,000 hits went.
