Data

Data NYT Resources Teaching

7 Ways to Explore the Math of the Coronavirus Using the New York Times

My latest piece for the New York Times Learning Network is “7 Ways to Explore the Math of the Coronavirus Using the New York Times”, a collection of ideas for using NYT articles, infographics, and interactives to explore the mathematics underlying the current coronavirus epidemic.

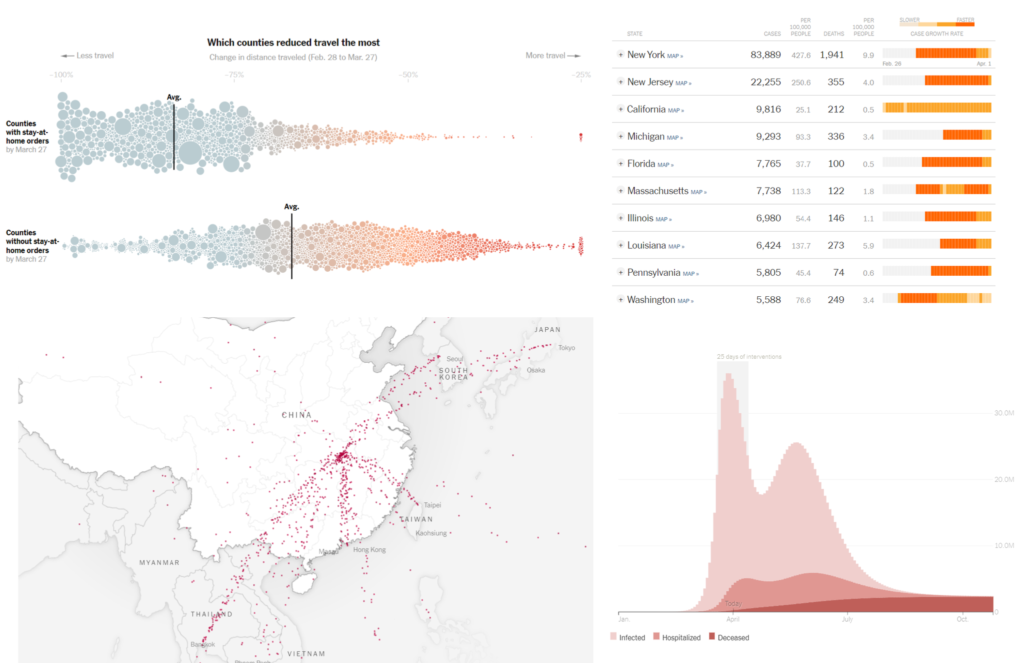
The opportunities range from statistical literacy to network theory. Here’s an example of some data analysis you can engage in using a wonderful NYT interactive:

By using sliders to change, for example, the level of intervention (e.g., moderate or aggressive) or the length of intervention (e.g., 14 days or 60 days), students can see how outcomes change. And, by playing with the model, they will be able to answer questions like: “What is the impact of shortening our social distancing period?” or “What happens when we delay the start of our interventions?”

The full article is freely available on the New York Times Learning Network.

By MrHonner, 5 years5 years ago

Data Geometry Resources Teaching

How Geometry, Data and Neighbors Predict Your Favorite Movies — Quanta Magazine

My latest column for Quanta Magazine makes a connection between high school geometry and recommendation engines used by companies like Netflix.

Adrienne is a Marvel movie fanatic: Her favorite films all involve the Hulk, Thor or Black Panther. Brandon prefers animated features like Inside Out, The Incredibles and anything with Buzz Lightyear. I like both kinds, although I’m probably closer to Adrienne than Brandon. And I might skew a little toward Cora, who loves thrillers like Get Out and The Shining.

Whose movie preferences are closest to yours: Adrienne’s, Brandon’s or Cora’s? And how far are your cinematic tastes from those of the other two? It might seem strange to ask “how far” here. That’s a question about distance, after all. What does distance mean when it comes to which movies you like? How would we measure it?

Using the perpendicular bisector–an elementary and underappreciated idea from high school geometry–we can carve up abstract data spaces into regions that can be fruitfully compared and contrasted. And knowing which region you lie in, and whom you are closest to, can help make predictions about your preferences.

To learn more, read the full article, which is freely available here.

By MrHonner, 5 years5 years ago

Appreciation Art Data Representation Teaching

2017 — My Year in Math

Dan Meyer recently shared a fun and telling graph describing his year in math. Inspired by Dan’s idea, and by a Math for America workshop with data visualization innovator Mona Chalabi, I created my own Year in Math entry. Though the real inspiration, I guess, came from the world events that made me want to read more books and less internet.

You can find more takes on the Year in Math theme on Twitter.

I think this could make for a fun student project. I hope the students agree!

By MrHonner, 7 years7 years ago

Data Representation

Birthday Frequency Visualization

This is a beautiful visualization of birthday frequency:

http://gizmodo.com/5910773/how-common-is-your-birthday

This “heat map” shows which days are the most common birthdays in the U.S.

Lost of interesting questions arise from this representation of data. We can immediately see that July, August, and September seem to form a disproportionate band of birthdays. And take a look at July 4th: what’s the explanation for that?

In addition, you could also use this chart to create some new twists on the classic birthday paradox!

By patrick honner, 12 years12 years ago

Data Representation Technology

Visualizing Ocean Currents

This is a beautiful representation of ocean currents around the world:

http://www.flickr.com/photos/gsfc/7009056027/

Put together by the NASA/Goddard Space Flight Center Scientific Visualization Studio, this short video circles the digital globe, showing the relative strengths and directions of ocean movement.

Watching this allows one to see some of the basic mathematics of fluid flow, like tendency toward rotation and how fluid behaves at boundaries. In addition, global phenomena like the jet stream and trade winds can also be perceived.

This dynamic representation of data is similar to this wind map in how it brings to life the ideas of vector fields and flow lines.

By patrick honner, 13 years4 years ago

Follow Mr Honner