Technology

Circumcircles in Desmos

Circumcircle in DesmosI’m presenting on Desmos at today’s AMAPS meeting in New York City, and preparing my talk was an object lesson in how wonderful this technology is.

Part of my presentation demonstrates simple ways that Desmos can be a part of every high school math class:  Algebra, Geometry, Trigonometry, Pre-Calculus, and Calculus.  While Geogebra is generally more suitable for demonstrating and exploring geometry, Desmos certainly can be useful in that course, so I wanted to show something relevant and interesting as part of my talk.  I thought, “Why not compute the circumcircle for an arbitrary triangle?”

While all the pieces of the mathematical puzzle were there for me, figuring out how to put them together in Desmos was a fun, frustrating, and worthwhile challenge.  I had to play around with the basic concepts associated with perpendicular bisectors and think creatively about some mathematical problems and equations.  I even ended up using the new regression feature in Desmos in a clever way!

I often get caught up in little challenges like this, and this is why Desmos is so wonderful:  it provides us a mathematical makerspace.  It invites us to play around, to create, to engineer, to build.  And all of this happens through using the language and concepts of mathematics.

You can see my circumcircle demonstration here, and you can find more of my work in Desmos here.

By MrHonner, ago

Derivatives of Vector Functions

Desmos -- Derivatives of Vector Valued FunctionsOne way to think of a curve in the plane (or in space) is as a collection of terminal points of vectors whose initial points are all at the origin.  The vectors are given by a vector-valued function.

For example, the parabola shown at right can be thought of as the graph of the vector-valued function

r(t) = < t , (t-1)^{2}+1>

I’ve created a Desmos demonstration that shows how graphs of vector-valued functions are related to their vectors (shown in blue), and how the derivative of a vector-valued function is related to both difference vectors and tangent vectors.  You can access the demonstration here.

You can find more of my Desmos demonstrations here.

By MrHonner, ago

Demonstration of Linear Independence

vectors spanning the plane

I’ve put together a simple Desmos interactive that demonstrates the basic ideas of linear independence.

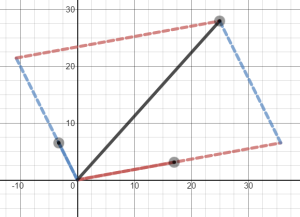
If two plane vectors are linearly independent, then every vector in the plane can be written as a linear combination of those two vectors.  Those two vectors span the plane.

By playing around with the sliders in this interactive, you can see how every vector in the plane can be expressed as a linear combination of the two original vectors.

Moreover, if you make the two original vectors parallel, they no longer span the plane.  That’s because the two original vectors are now linearly dependent!  Each is a linear combination (in this case, a scalar multiple) of the other.

You can see this Desmos interactive here, and you can find more of my Desmos-based demonstrations here.

By MrHonner, ago

3D Printing in Calculus Class

I’m looking forward to exploring 3D printing in Calculus class this year.  We don’t have a printer in our classroom (yet!), but some students have enough experience and access to work on modest projects outside of class.

Here’s a print of an interesting surface in xyz-coordinate space.

Beautiful Surface and Printed SurfaceIt’s always exciting to find a new way to represent or experience a mathematical idea, and physical representations can be especially powerful.

And perhaps more importantly, 3D printing gives students an opportunity to use mathematics to create.  Mathematics is a creative endeavor, and whatever helps promote this idea will ultimately help change attitudes about math.

 

By MrHonner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: