I’ve been enjoying getting familiar with our new 3D printer. I’m not sure these parametric surfaces were the best pieces to start out with, but I have learned a lot!
From left to right, we have a figure eight torus, a Fresnel surface, and a cyclide. Not pictured: the many, many failures.
At Math for America’s most recent Master Teachers on Teaching event, I presented “When Technology Fails”, a short talk about how my personal and professional experiences have shaped the way I view and teach technology.
The failure of technology has been a consistent part of my personal and professional computing experience. These failures have served as excellent learning opportunities, and perhaps more importantly, they have instilled in me a healthy distrust of technology.
As a teacher, I find students far too trusting of technology. Often, they accept what their calculators or computers tell them unthinkingly. In my talk, I discuss how we can make students conscious of the shortcomings of technology in ways that create meaningful learning opportunities. And hopefully, by confronting the failures of technology head on, students will develop a healthier attitude about what technology can, and can’t, do.
A video of “When Technology Fails” can be viewed here. And a talk I gave at a previous MT^2 event, “g = 4, and Other Lies the Test Told Me”, can be seen here.
I’m presenting on Desmos at today’s AMAPS meeting in New York City, and preparing my talk was an object lesson in how wonderful this technology is.
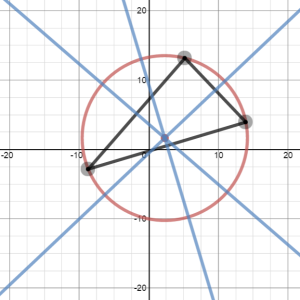
Part of my presentation demonstrates simple ways that Desmos can be a part of every high school math class: Algebra, Geometry, Trigonometry, Pre-Calculus, and Calculus. While Geogebra is generally more suitable for demonstrating and exploring geometry, Desmos certainly can be useful in that course, so I wanted to show something relevant and interesting as part of my talk. I thought, “Why not compute the circumcircle for an arbitrary triangle?”
While all the pieces of the mathematical puzzle were there for me, figuring out how to put them together in Desmos was a fun, frustrating, and worthwhile challenge. I had to play around with the basic concepts associated with perpendicular bisectors and think creatively about some mathematical problems and equations. I even ended up using the new regression feature in Desmos in a clever way!
I often get caught up in little challenges like this, and this is why Desmos is so wonderful: it provides us a mathematical makerspace. It invites us to play around, to create, to engineer, to build. And all of this happens through using the language and concepts of mathematics.
You can see my circumcircle demonstration here, and you can find more of my work in Desmos here.
One way to think of a curve in the plane (or in space) is as a collection of terminal points of vectors whose initial points are all at the origin. The vectors are given by a vector-valued function.
For example, the parabola shown at right can be thought of as the graph of the vector-valued function
I’ve created a Desmos demonstration that shows how graphs of vector-valued functions are related to their vectors (shown in blue), and how the derivative of a vector-valued function is related to both difference vectors and tangent vectors. You can access the demonstration here.
You can find more of my Desmos demonstrations here.
I was playing around in Scratch this weekend, experimenting with some numerical methods for approximating integrals, when this lovely image unexpectedly emerged. I call it Twilight on Mars.
Twilight on Mars
Looks like I’ve got a new math and art project for students, and me, to explore!
