I have enjoyed analyzing and writing about the strategy implications of the NFL’s Playoff Overtime rules, and we’ve seen those rules in action for the first time this year.
Here’s a short summary: the first possession in overtime is determined by a coin flip. The first-possessing team will be known as Team A, and the other team will be Team B. If Team A scores a touchdown, they win immediately; if Team A scores a FG, then Team B will receive the ball and can win (with a TD), tie (with a FG), or lose (with a turnover). Aside from the specific first- and second-possession situations governed by these rules, the rest of overtime plays out in classic sudden-death style.
I looked closely at whether it is useful for Team A to attempt a FG, but the question that occurred to me recently was “If you win the coin toss, is it obvious that you want the ball first?”
Consider the following chart. Again, Team A is the first-possessing team, and Team B is the other team. The chart shows all the possible sequences of outcomes on the first two possessions: touchdown (TD), field goal (FG), or Turnover. Here, a turnover could be a fumble, and interception, a punt, or a turnover on downs.
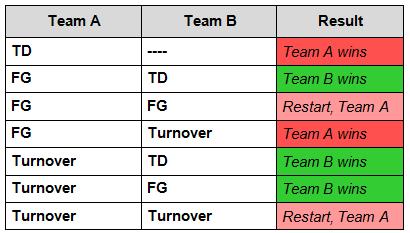
The first-possessing team, Team A, certainly has an advantage in that they can end the game immediately by scoring a touchdown. But if they don’t score a touchdown, Team B can always win with a TD and in some cases can win with only a FG! Furthermore, as the original kickoff team, Team B may enjoy a strategic advantage in field position, which can further affect the above scenarios.
Now, in all situations where the game is not decided within the first two-possessions, Team A gets the ball first as sudden-death rules take over. However, I recall analyses that suggest that the first possessing team doesn’t have a statistically significant advantage in sudden-death overtime.
This is an admittedly elementary look at the situation, but it seems to me that the answer to the question “Do we want the ball first in OT?” is not obvious. Hopefully I’ve given the coaches something to think about this week.
Related Posts
As one who prides himself on his quantitative reasoning abilities, I am embarrassed at how poorly I manage my Metrocard.
