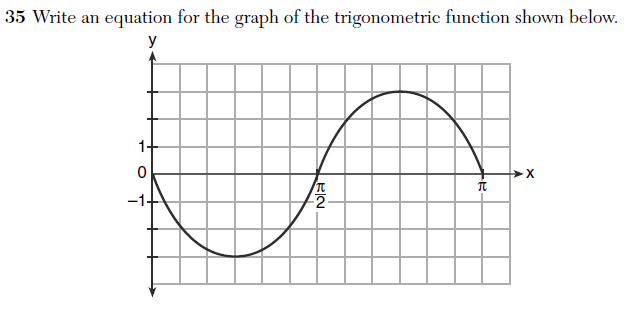
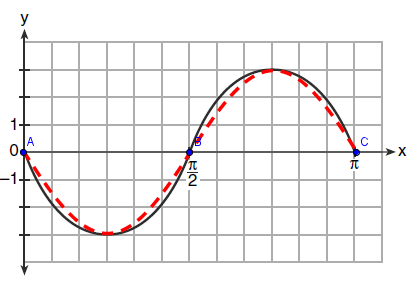
Upon discovering that I had been paying much more for my coffee than I realized, I was faced with a dilemma only algebra could solve. Or, at least help analyze.
You see, my local coffee shop offers a simple reward program for regular customers: purchase 10 bags of coffee, and your eleventh bag is free. At the time of my discovery, I had credit for four bags of coffee. Thus, the dilemma: do I continue to buy the over-priced coffee six more times in order to get the free bag? Or do I just start buying cheaper coffee somewhere else?
The coffee at my local shop was costing me around $12 for 12 ounces. I knew I could get comparable coffee at another shop for around $10 a pound. So should I stay or switch?
If I bought 6 more bags from the local shop, I’d spend $72 and get seven 12-ounce bags of coffee (the six I bought, and the free one). Thus, I would get 84 ounces of coffee for $72.
Now $72 dollars at the new place would get me 7.2 pounds of coffee, or around 115 ounces. So I’d be getting an additional 31 ounces, or almost two pounds of coffee, by switching!
Needless to say, I swtiched. But it got me thinking: at what point would it have been better to continue buying the over-priced coffee? I turned to algebra for the answer.
Let x = the number of bags of coffee that have already been purchased. In order to get a free bag of coffee from my local shop, I’d need to buy ten total bags; thus, I’d need to purchase (10 – x) more bags of coffee. After that, I’d receive one free bag, so in the end I’d get (10 – x + 1) = (11 – x) total bags of coffee.
Each 12-ounce bag of coffee costs $12, so I’d spend a total of $12 * (10 – x) to get (11 – x) * 12 ounces of coffee.
This works out to a price of
dollars per ounce
for the coffee I’d get from the old place.
I know I can get coffee at the other place for $10 per pound, or 
dollars per ounce. Thus, I want to find x so that
which would mean that the coffee from the old place would be cheaper per ounce than the coffee from the new place.
Now we simplify our inequality:
,
,
,
Thus, I should continue buying coffee at the old place if I’d already bought more than eight bags of coffee there. Otherwise, I’d be better off switching.
I probably didn’t need algebra to tell me to stick with the old place if I’d already bought 9 bags, but algebra did show me just how hopeless my situation was!
Related Posts
