Through Math for America, I am part of an on-going collaboration with the New York Times Learning Network. My latest contribution, a Test Yourself quiz-question, can be found here:
http://learning.blogs.nytimes.com/2010/09/27/test-yourself-math-sept-27-2010/
This problem was based on an article discussing weak and strong passwords, a subject near and dear to any cryptographer’s heart.
This article, the first in a series about drawing, is about how important the ellipse is to the artist.
http://opinionator.blogs.nytimes.com/2010/09/23/the-frisbee-of-art/
The author gives a nice, if long, explanation about the significance of the ellipse, but it basically boils down to this: circles are everywhere. And often, when we are looking at circles, we’re looking at them atilt. We see projections of the circle, and projections of circles are ellipses.
Think of it this way: suppose you have a hula hoop and you hold it parallel to the ground. The shadow you see is circular, but if you tilt the hula hoop, the shadow will change–into an ellipse.
I don’t have a hula hoop, so I made do with a key ring:
As the circular key ring is rotated, it becomes less parallel to the ground; the shadow becomes less circular and more elliptical. And at the end, the ellipse vanishes–an ellipse eclipse!
After reading a post about 3-D printers, I found out about this assemble-it-yourself 3-D Printer!
http://reprap.org/wiki/Main_Page
Not only is the RepRap cheap to build (people claim it can be done for around $400), but all the software and hardware designs are open-source and free.
But it doesn’t stop there. If you already have a RepRap, you can use it to build some of the parts you to build another RepRap! In other words, this is a self-replicating machine! Well, partially at least.
I’m sure there are plenty of people out there with the skills to build one of these themselves. I’m not sure I’m one of them–after all, building a table that was almost level was a huge success for me. But this is such a cool idea it might just be worth a shot!
A lot of people spend a lot of time trying to understand stock prices: Are they predictable? Are they random? Can you make money by identifying trends? Can you beat the market and make a fortune?
A prevailing theory is that stock prices are essentially random walks; that is, no more predictable than a coin flip. The amount a price goes up or down at any given moment might follow some pattern (small movement is more likely than large movement, for example), but whether that movement is up or down is basically random. Now, what random means to mathematicians can get kind of complicated, but that’s another story.
I thought it might be interesting to compare actual stock prices to a randomly-generated trend line. After playing around with a spreadsheet and experimenting with different parameters, I produced the following two graphs:
One of these graphs represents 200 days of prices of the Dow Jones Industrial average; the other represents a quantity that moves up or down randomly, by some random amount. Figuring out how to get a good-looking random graph took some time, and is an interesting challenge in and of itself.
So, can you tell which is the Dow and which is a coin toss? More importantly, how much would you be willing to bet on it?
Related Posts
I enjoy offering impossible problems to students as extra credit, although I usually don’t tell them the problems are impossible. Such tasks usually engage them, confuse them, and make them suspicious of me. It’s a win-win-win.
While discussing some three-dimensional geometry, I offered extra credit to anyone who could build a model of a Klein bottle. The Klein bottle is a hard-to-imagine surface that has neither an inside nor an outside. It’s like a tube where one end meets the other and makes a seal, but somehow got turned inside out in the process. If you are familiar with the Mobius strip, the Klein bottle is basically a higher-dimensional Mobius strip.
One reason that the Klein bottle is hard to visualize is that it can’t be observed in three dimensions: it needs a fourth dimension in order to see it turn itself inside-out. This is analogous to the standard construction of the Mobius strip: we take a long strip of paper, give one end a half-twist, and tape the ends together. We think of the paper itself as being 2-dimensional, but we need that third dimension to twist through.
So, I was pretty impressed with the student who made this.
Not bad at all, for someone who is dimensionally challenged. Here’s a nice representation for comparison, although it’s still a cheat. The Klein bottle doesn’t really intersect itself.
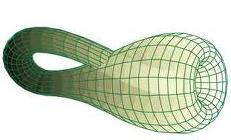
A nice example of impossibly creative student work!