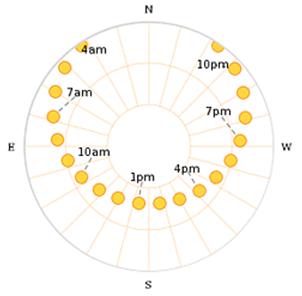
 Here’s a cool article from the Wolfram Alpha Blog about using WolframAlpha to plot the sun’s path, as seen from various locations:
Here’s a cool article from the Wolfram Alpha Blog about using WolframAlpha to plot the sun’s path, as seen from various locations:
http://blog.wolframalpha.com/2010/09/22/following-the-suns-unique-path/
You can also alter the date, which means you can look at historical data or projected future data.
Unfortunately, when I tried the command “sunpath north pole” (employing the classic mathematical strategy consider extreme cases), WolframAlpha gave me the sun path for North Pole, Alaska, a very oddly named place as it is nowhere near the actual North Pole.




