Are You Related to Confucius?

Are all of us descendants of Confucius?  Here’s a curious mathematical argument that suggests just that.

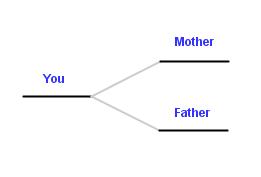
No matter who you are, you came from a mother and a father (I won’t go into details).  So, in your family tree, the part behind you has two branches, like this:

family tree 1

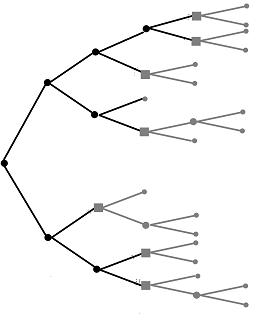
The same goes for your mother and father, and their mothers and fathers, and so on.  Thus, continuing on back the line, you see a family tree like this

binary tree

And it just keeps going and going and going.  An interesting mathematical feature of this tree is that, as your move backward in time, each generation has twice as many branches as the previous generation, roughly speaking.  Thus, when you go back a hundred or so generations, to the time of Confucius, the number of branches in your family tree is roughly 2^{99}, or 633,825,300,114,114,700,748,351,602,688 (thanks, WolframAlpha).

A reasonable estimate is that at the time of Confucius there were around 250 million total people in existence.  Each of those 2^{99} spots in your family tree has to be filled by someone, which means that, on average, each person in existence at that time had to fill roughly

\frac {2^{99}} {250,000,000} =  2,535,301,200,456,458,802,993

of the spots in your family tree.   It seems like a statistical impossibility that Confucius wasn’t one of them.  So, I guess that makes us cousins?

By patrick honner, ago

Math at the Boundary

While in Maine, I took some nice photos of the boundary between the beach and the sea:

Shoreline

It made me think of something I saw a long time ago (maybe on 60 Minutes?) about a scientist who thought deeply about coffee spills on his countertop. The power of the internet helped me locate Sidney Nagel, a physicist who studies the physics of drops, why things get “jammed”, and why a coffee spill leaves a dark ring after it dries.

Is there any way to predict the kind of edge this water will make as it crawls up the beach? Is there any order in this chaos? If this inspires you to great scientific accomplishment, please remember where you got your start.

By patrick honner, ago

The Levytator

LevytatorFrom the “Why Didn’t I Think of This?” files comes the Levytator,

http://www.youtube.com/watch?v=iC_se2zrmLM

The Levytator is a more efficient and flexible take on the escalator.  It runs in a circuit, instead of conveyor-belt style, so you don’t lose half your steps to the useless, upside-down underground path, like in a traditional escalator.  Thus, you get more transportation per square foot of step.

In addition, the interlocking steps are curved and not rectangular, meaning that not only can the Levytator turn around corners, but essentially it can be designed to follow any kind of path a planner might need.

Be sure to check out the video for some cool demonstrations (which remind me a lot of closed-loop integrals).

By patrick honner, ago

The Art of the Ellipse

ellipse -- conicThis article, the first in a series about drawing, is about how important the ellipse is to the artist.

http://opinionator.blogs.nytimes.com/2010/09/23/the-frisbee-of-art/

The author gives a nice, if long, explanation about the significance of the ellipse, but it basically boils down to this:  circles are everywhere. And often, when we are looking at circles, we’re looking at them atilt.  We see projections of the circle, and projections of circles are ellipses.

Think of it this way:  suppose you have a hula hoop and you hold it parallel to the ground.  The shadow you see is circular, but if you tilt the hula hoop, the shadow will change–into an ellipse.

I don’t have a hula hoop, so I made do with a key ring:

Ellipses

As the circular key ring is rotated, it becomes less parallel to the ground; the shadow becomes less circular and more elliptical.  And at the end, the ellipse vanishes–an ellipse eclipse!

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: