Teaching

Resources Student Work Teaching Technology

Student Desmos Projects

Desmos, the free, browser-based graphing utility, has quickly become an indispensable tool in the mathematics classroom. It provides easy, intuitive access to graphs of functions and relations, and creates unique opportunities to understand mathematical relationships dynamically.

But to me, its greatest virtue may be that Desmos provides opportunities to use mathematics to create. I like to think of Desmos as a mathematical makerspace, where the tools at our disposal are exactly the tools of mathematics.

To that end, when I introduce students to Desmos, we always work toward the creation of something mathematical. Below are some beautiful examples of student work from our latest round of Desmos projects.


Varignon’s Theorem	Vector Projections


Angle Bisector Theorem	Three Lines Intersecting

You can find more of my work with Desmos here.

By MrHonner, 9 years9 years ago

Statistics Teaching Testing

Regents Recap — August 2015: Modeling Data

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Data and statistics play a much bigger role in algebra courses now, due in part to their increased emphasis in the Common Core standards. I am generally supportive of this, but I do worry about how statistical concepts are presented and assessed in these courses and on their exams.

For example, here is question 27 from the August, 2015 Common Core Algebra exam.

Evaluating mathematical models is an extremely important skill in many aspects of life. But properly evaluating mathematical models is subtle and complex.

The following sample response, provided by New York state as an example of an answer deserving of full credit, does not respect that complexity. And it makes me worry about what we are teaching our students about this important topic.

It’s true that the given data does not grow at a constant rate. But that isn’t a good reason to reject a linear model for this set of data. Models are used to approximate data, not represent them perfectly. It would be unusual if a linear model fit a real set of data perfectly.

The weakness of this argument becomes even more apparent when we notice that the data isn’t perfectly fit by an exponential model, either. Therefore, how could it be wrong for a student to say “We should use a linear model, because the data doesn’t grow at a linear rate and thus isn’t exponential”?

This is another example of the problems we are seeing with how statistics concepts are being handled on these high stakes exams, which is a consequence of both the rushed implementation of new standards and an ever-increasing emphasis on high-stakes testing in education. It is also an example of how high-stakes tests often encourage terrible mathematical habits in students, something I address in my talk “g = 4, and Other Lies the Test Told Me“.

Related Posts

By MrHonner, 9 years8 years ago

Geometry Teaching Testing

Regents Recap — August 2015: Trouble With Transformations

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The Common Core Geometry standards emphasize a transformation-based approach to congruence and similarity. This is not a new mathematical idea, but it is novel in the context of traditional high school geometry.

How transformation-based geometry is assessed has been an on-going concern, and this question from the August 2015 Common Core Geometry exam highlights some of the mathematical concerns.

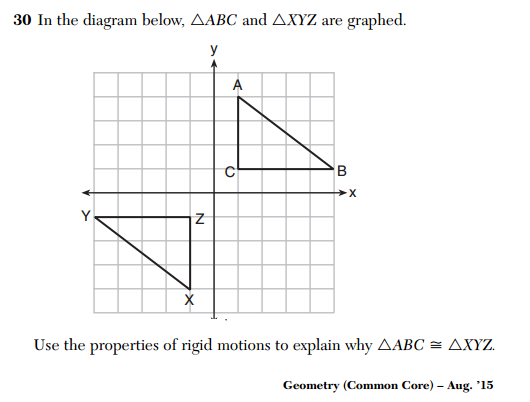
The student is supposed to argue that one of these triangles is the image of the other triangle under some rigid motion, and since rigid motions preserve length and angle, the image is congruent to the original.

But the following work samples, provided by New York State as examples of full-credit responses to this problem, demonstrate a serious lack of appreciation for the mathematics involved in this argument.

Notice that no attempt has been made to justify that a mapping that takes triangle ABC onto triangle XYZ exists, which is the foundation of this argument. The existence of such a mapping is merely stated as fact.

This full-credit response makes no reference to any specific triangle at all. It merely states a general property of rotation.

Ironically, the sample zero-credit response offered by the state is the most complete and rigorous response of all.

Here, the student has made a full, appropriate congruence argument, but receives no credit because they did not appeal to rigid motions.

I understand the desire to assess specific content and techniques, but in these sample response items, the state makes some curious decisions about who will be rewarded and who will be penalized. A student trained to simply regurgitate facts about rigid motions (“Rigid motions preserve distance”) is rewarded, while a student who actually attempts to solve the specific problem at hand, demonstrating depth of knowledge (and, perhaps, flexibility) in the process is penalized.

It’s not hard to imagine the consequences this can have on teaching and learning. These unintended, and typically unmentioned, consequences result from rushed policy implementation and over-emphasis on testing, and in many ways work to undermine the work of students and teachers.

By MrHonner, 9 years ago

3D Printing Resources Student Work Teaching

3D Printing in Math Class

We were fortunate to receive a 3D printer for use in our math class midway through the last school year. Figuring out how it best worked was fun, and often frustrating.

We enjoyed a variety of successes throughout the spring, printing simple surfaces and some complicated ones, too. It was fascinating to uncover how the printer, and its software and hardware, tackled certain engineering obstacles, like how to print in mid-air!

Ultimately I got comfortable enough to start producing some lesson-specific mathematical objects. This trio of solids I designed worked perfectly as an introduction to Cavalieri’s principle: seeing and holding the objects immediately initiated the conversations I wanted students to have.

By the end of the school year, I felt comfortable enough with the process to run our first official student project. It was fairly open-ended, with options for students, but essentially the idea was to design an object for printing using equations and inequalities.

The project was a success, and here are some of the student designs.

I’m looking forward to exploring some new ideas and projects this year. It’s clear to me that this technology, which is fundamentally mathematical in concept and design, can play a valuable and meaningful role in math class.

By MrHonner, 9 years9 years ago

Teaching Testing

Regents Recap — August 2015: Common Core Algebra

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The August 2015 administration of the Common Core Algebra exam was similar in style, content, and difficulty to the prior Common Core Algebra exams. There are a few interesting trends emerging.

Harder Multiple Choice

As part of the general increase in difficulty of these exams, we are seeing harder types of multiple choice questions. Here are questions 9 and 21:

The simplest kind of multiple choice question in this style might just ask “Which of the following statements is true?” It is generally more difficult to instead identify a false statement among a set, or to correctly identify the true or false subset of statements from a set. I don’t object to these kinds of questions, but it’s worth acknowledging that this is one subtle way in which the difficultly of the exam can be tweaked.

Confusing Contexts

On each of the Common Core Algebra exams thus far, there have been real-world problems that I found very confusing. In some cases, the more I read them, the less I understood what the question was asking. Here is Question 18:

Apart from the decidedly unrealistic real-world context, I was quite confused about whether we were interested in monthly payments or total payments. I wonder if these kinds of problems confuse students, or if they have just [properly] learned to ignore the model and just figure out what the test-maker wants to hear.

Physics

We have seen some Calculus-style content moved down into this Common Core Algebra exam. Here, in Question 28, students are essentially asked to graph an antiderivative.

2015 August CC Alg 28 I don’t have any philosophical objections to this particular content being part of an 8th- or 9th-grader’s mathematical experience, provided it’s part of a coherent curriculum. But I do wonder about the inherent fairness of this as an 8th- or 9th-grade math exam question.

This question assesses an important concept in introductory physics. Students in schools where Physics is taught in 9th grade will have a significant advantage on this kind of problem, while other students are in danger of being rated lower on mathematical proficiency simply because they haven’t taken physics.

This is another example of the virtually infinite set of confounding variables involved in assessing learning and teaching.

By MrHonner, 9 years9 years ago

Follow Mr Honner