Regents Recap — August 2015: Trouble With Transformations
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
The Common Core Geometry standards emphasize a transformation-based approach to congruence and similarity. This is not a new mathematical idea, but it is novel in the context of traditional high school geometry.
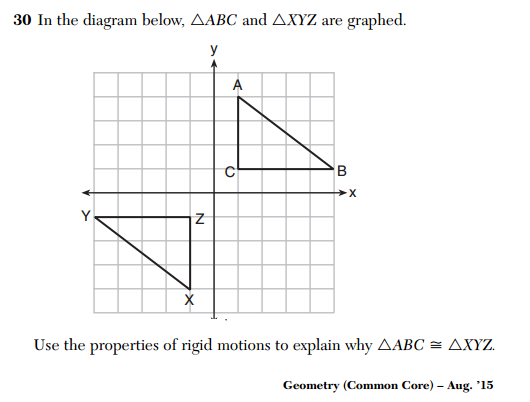
How transformation-based geometry is assessed has been an on-going concern, and this question from the August 2015 Common Core Geometry exam highlights some of the mathematical concerns.
The student is supposed to argue that one of these triangles is the image of the other triangle under some rigid motion, and since rigid motions preserve length and angle, the image is congruent to the original.
But the following work samples, provided by New York State as examples of full-credit responses to this problem, demonstrate a serious lack of appreciation for the mathematics involved in this argument.
Notice that no attempt has been made to justify that a mapping that takes triangle ABC onto triangle XYZ exists, which is the foundation of this argument. The existence of such a mapping is merely stated as fact.
This full-credit response makes no reference to any specific triangle at all. It merely states a general property of rotation.
Ironically, the sample zero-credit response offered by the state is the most complete and rigorous response of all.
Here, the student has made a full, appropriate congruence argument, but receives no credit because they did not appeal to rigid motions.
I understand the desire to assess specific content and techniques, but in these sample response items, the state makes some curious decisions about who will be rewarded and who will be penalized. A student trained to simply regurgitate facts about rigid motions (“Rigid motions preserve distance”) is rewarded, while a student who actually attempts to solve the specific problem at hand, demonstrating depth of knowledge (and, perhaps, flexibility) in the process is penalized.
It’s not hard to imagine the consequences this can have on teaching and learning. These unintended, and typically unmentioned, consequences result from rushed policy implementation and over-emphasis on testing, and in many ways work to undermine the work of students and teachers.



8 Comments
Dave Marain · October 9, 2015 at 11:46 am
Do they also release the scoring rubric so we know what was expected from the item writers? From my experience the 1st sample response, but not the 2nd, would normally get full credit. The student could have added more detail of how the rotation would map the vertices using coordinates but I’m not sure that was expected. That’s why the rubric would help. I wholeheartedly agree with you re rushed implementation and over testing but that’s an issue separate from the mathematical validity of the question, the rubric and the scoring. I’m intrigued by the 1st student’s decent use of math terminology and ability to write a coherent argument!
MrHonner · October 9, 2015 at 3:03 pm
Everything that is publicly released can be found here, which includes a rating guide.
While the first sample response demonstrates solid mathematical technique, it completely glosses over the most important element in proving congruence via transformation. Moreover, simply saying something is true without justifying it, or even acknowledging that it needs to be justified, is not what we should be training mathematics students to do.
The issues here are not separate from standards and testing. The rush to implement new standards means we are teaching and testing material that is clearly not understood by those in charge, as evidenced by these full-credit sample responses. The culture of over-testing contributes to this, as well, because what seems to matter only is that students take tests, not that we spend time and resources to develop meaningful assessments.
Dave Marain · October 9, 2015 at 4:17 pm
Thanks for the links. Pls remember we’re on the same side! The trouble is that my level of frustration and anger over these assessments is tempered by age and years of raging at the machine back in the 90’s and early 21st century! I need you to spell out for me “the most important element in proving congruence” that was missed by the sample response. This student, if real, has limited time to flesh out an explanation and knows that it will earn a ‘2’ as is. I think you might be more upset over what the committee’s expectations were and the inherent limitations of these kinds of tests. Of course we want to see a deeper understanding of concepts but, imo, that takes place in formative assessment in the classroom. If you’re arguing that these tests are damaging kids and their learning, you’re dead-on. Keep fighting the fight! Dave Marain
ben · October 11, 2015 at 12:55 am
I’m with Patrick. The samples assume congruence and then restate the congruence is maintained during the rotation. To be done properly you must show after rotation the two triangles overlay.
Dave Marain · October 11, 2015 at 12:53 pm
And you do that how, Ben? Find the rotation image of each vertex? The Regents committee should comment on this and explain WHY that was not required! My guess is that on a 3-point rubric 0,1,2) this wasn’t expected. However, “SHOULD it have been expected?” requiring the student to demonstrate deeper understanding of congruence? Probably, but is that made clear in the directions to the student? I don’t think so. I still believe we’re reacting more to what is NOT EXPECTED by the test makers and the need for more mathematical validity. Students will generally do no more than what they believe is expected, not what you and I expect! The issue then is how these expectations are delineated by the committee and communicated clearly to teachers and, in turn, the students. All of us have the same goal here. The rub is in the implementation and the rush to assessment has subverted these goals. We’re preaching to the choir here when we’re all on the same side…
David Griswold · October 13, 2015 at 4:10 pm
I’m interested in this, as I think transformation-based congruence conversation SEPARATE from algebraic geometry is interesting, but I don’t know much about it. Would this, in your opinion, be a better argument?
We can see that AC=ZX and BC=ZY and that <A=<Z=90 degrees. Translate ABC (creating image A'B'C') such that C' lies on top of Z. Now rotate A'B'C' (creating new image A''B''C'') such that C''B'' lies on top of ZY. Since lengths are preserved in rigid motions, we know that C''B''=ZY, so therefore B must lie on top of C. Since angles are preserved, we know that ray C''A'' lies on top of ray ZX, and since C''A''=ZY, we also know that A'' lies on top of Y''. Therefore, A'' lies on top of X, B'' lies on top of Y, and C'' lies on top of Z, so the A''B''C'' is congruent to XYZ and ABC is therefore congruent to XYZ.
David Griswold · October 13, 2015 at 4:12 pm
Dang it! Notation errors. I meant “B” must lie on top of Y” and “A” lies on top of X”. But you get the drift.
MrHonner · October 13, 2015 at 8:04 pm
David-
Yes, this is one approach that works, and the composition of the translation and the rotation is conceptually straightforward. I like to show this approach to students.
Generally speaking, if two congruent objects have the same orientation, then one can be mapped onto the other using only a single rotation or a single translation. Here, a single rotation (180 degrees about the origin) obviously works.
You could establish this by noticing that AX, BY, and CZ all have the origin as a midpoint. Therefore, you can rotate 180 degrees about the origin taking A to X, B to Y, and C to Z. You could also invoke the algebraic nature of rotation by 180 degrees about the origin (or reflection through the origin), namely that R: (x,y) -> (-x,-y) to draw the same conclusion.