My latest piece for the New York Times Learning Network is a math lesson that uses Elizabeth Green’s article “Why Do Americans Stink at Math?” to get students thinking about the most effective ways to teach and learn mathematics.
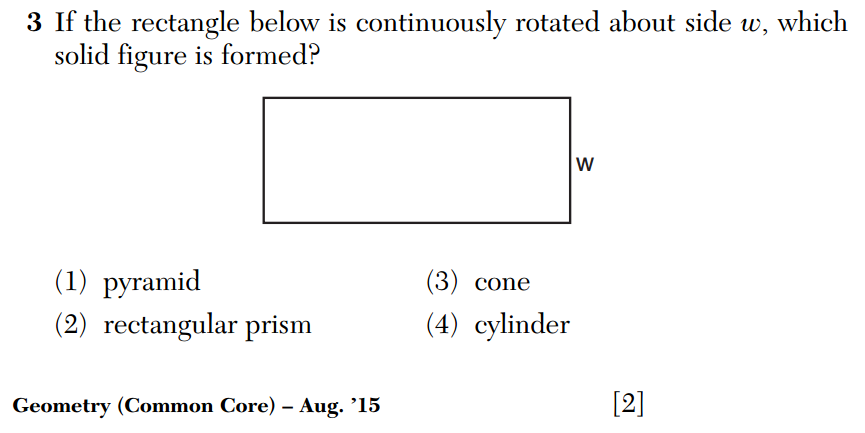
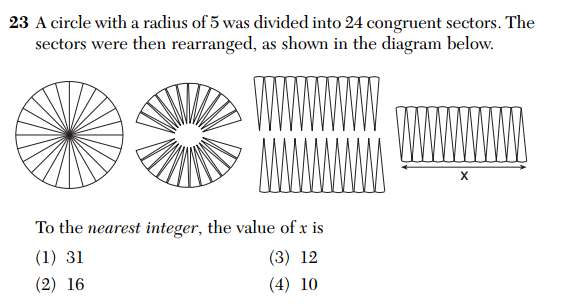
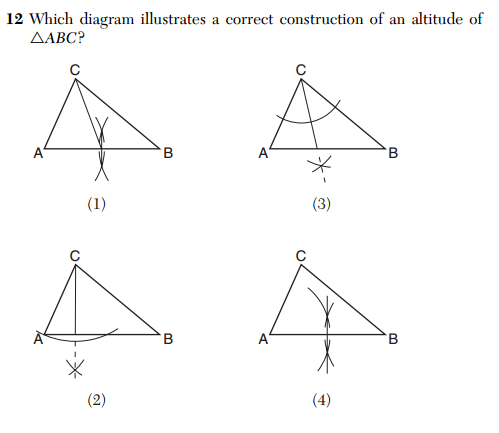
Is there a crisis in math education? Lots of people seem to think so.
From worries about where the United States ranks on international tests to arguments over the Common Core, the way teachers teach and students learn math continues to be debated widely, leading to proposed changes in the ways mathematics is taught. But what really works for students in the math classroom? And when changes to the techniques are necessary, how can they be implemented effectively and appropriately across an entire system? This Text to Text lesson plan confronts those questions and more.
Students are invited to use the suggested texts, as well as their own experiences in math class, to explore questions like “Do you believe teaching with a stronger emphasis on conceptual understanding will improve students’ performance in math?”, “What are some of the potential obstacles one might face in trying to change the way mathematics, or any subject, is taught?”, and ultimately, “What are the best ways to teach and learn mathematics?”
The entire piece is freely available here. There are already a number of interesting student comments on the piece. It’s certainly eye-opening hearing what they have to say about how they perceive effective math teaching.
