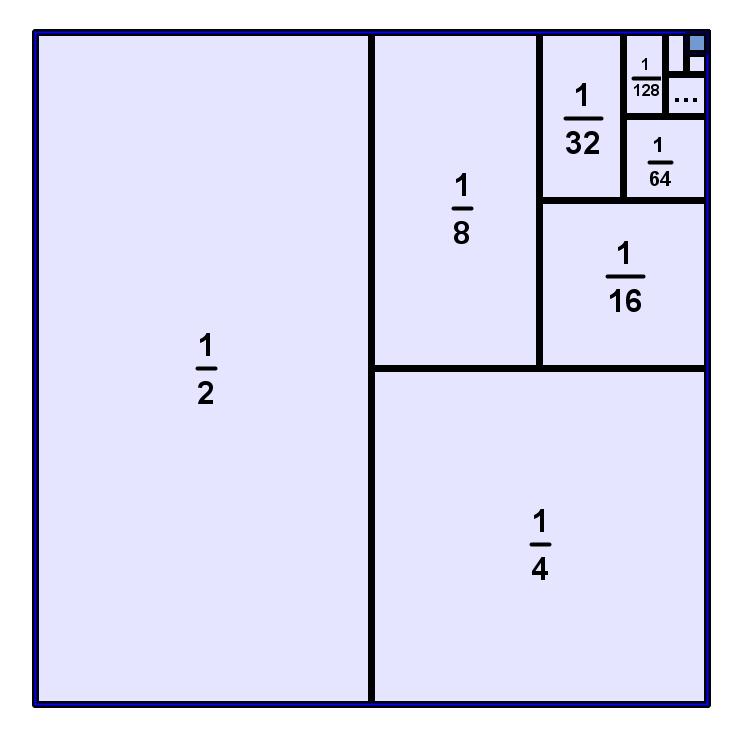
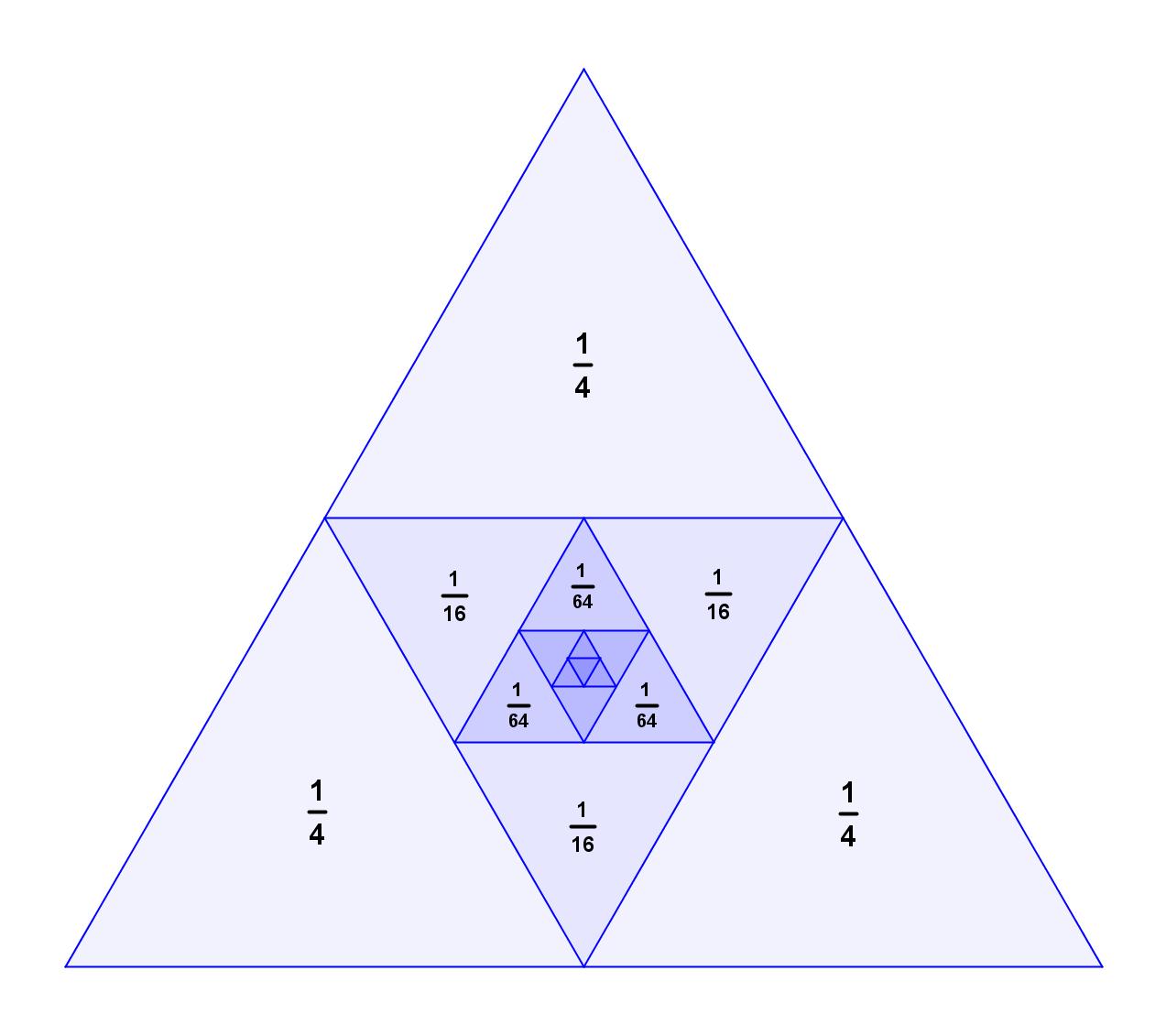
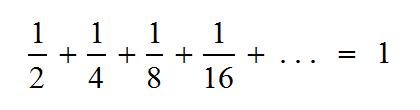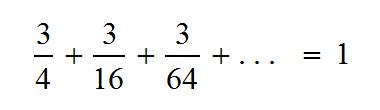Appreciation

Appreciation Geometry

Twirling Tori

This is a mind-blowing animation of arms circulating around a torus, created by Emilio Gomariz. I definitely became entranced for a bit, trying to follow a single hand all the way around the donut. (Click the image or this link if you can’t see the animation).

Apart from being visually amaazing, this puts me in mind of a result about fluid flows on surfaces. This animation demonstrates that a liquid, for example, can flow over the surface of a torus in such a way that every point moves: nothing appears stationary here, and everything is moving in a smooth (i.e., continuous) fashion.

The remarkable result is that this same can not be done on the surface of a sphere! There will always (at least) one point on the surface of the sphere that doesn’t move. A popular interpretation of this result is that however windy it might be outside, there is always at least one point on the Earth that is perfectly calm.

By patrick honner, 14 years9 years ago

Appreciation Challenge Geometry

Proofs Without Words

Here are two of my favorite Proofs Without Words. I’ve been thinking about infinite geometric series a lot lately, and these are two lovely, well-known, visualizations of two amazing infinite sums:

In a square of side length 1 (and therefore, area 1), cut the square in half; then cut one half in half (that’s a quarter); now cut one of the quarters in half (that’s an eighth); and so on and so on and so on (this puts the infinite in infinite sum). Eventually you’ll fill up the whole square! So this is a demonstration of the following amazing, and somewhat counterintuitive, fact that

Similarly, this diagram

is a visual representation of the following sum:

As any good, lazy mathematician would say, the details are left to the reader.

Appreciation Probability

Paul the Octopus, 2008-2010

Paul the Octopus, whose prognosticating skills captured the imaginations of World Cup viewers everywhere, died this week at the age of 2.5. He died of natural causes.

Paul defied probability by correctly predicting the results of all of Germany’s seven World Cup matches. After making it through the tournament with a perfect record–during which he received death threats and had a stamp printed in his honor–Paul retired from predicting. Rediscovering his British roots, Paul was appointed an official ambassador for England’s 2018 World Cup bid, a post he held until his untimely demise.

Apparently there have been many copy-cats, so to speak, including “a saltwater crocodile named Dirty Harry, who predicted Spain’s World Cup final win and called the result of Australia’s general election by snatching a chicken carcass dangling beneath a caricature of Prime Minister Julia Gillard”. But Paul will always have a special place in our hearts.

By patrick honner, 14 years9 years ago

Appreciation Art Geometry

Wireframe Torus

This is a cool example of wire-sculpture: a single piece of wire woven into the shape of the torus.

http://makezine.com/2010/10/24/math-monday-wire-torus-challenge/

(I doubt you can play pool on this one, though.)

The author of the blog post, George Hart, is the proprietor of the soon-to-be Math Museum, and it seems he is something of a sculptor himself. According to the article, this piece was on display at a conference held by the European Society for Mathematics and the Arts.

Poking around their website and admiring the the multitudinous mathart is a pleasant way to pass a little time.

By patrick honner, 14 years9 years ago

Appreciation Geometry

More Triangle Appreciation

It’s been a great week for special triangles.

Six days ago was a rare Equilateral Triangle day, four days ago we appreciated the 10-12-10 triangle, and today, 10/16/10, gives us another triangle to admire.

It’s actually very closely related to the 10-12-10 triangle, which we saw is just two right triangles pasted together.