Proofs Without Words
Here are two of my favorite Proofs Without Words. I’ve been thinking about infinite geometric series a lot lately, and these are two lovely, well-known, visualizations of two amazing infinite sums:
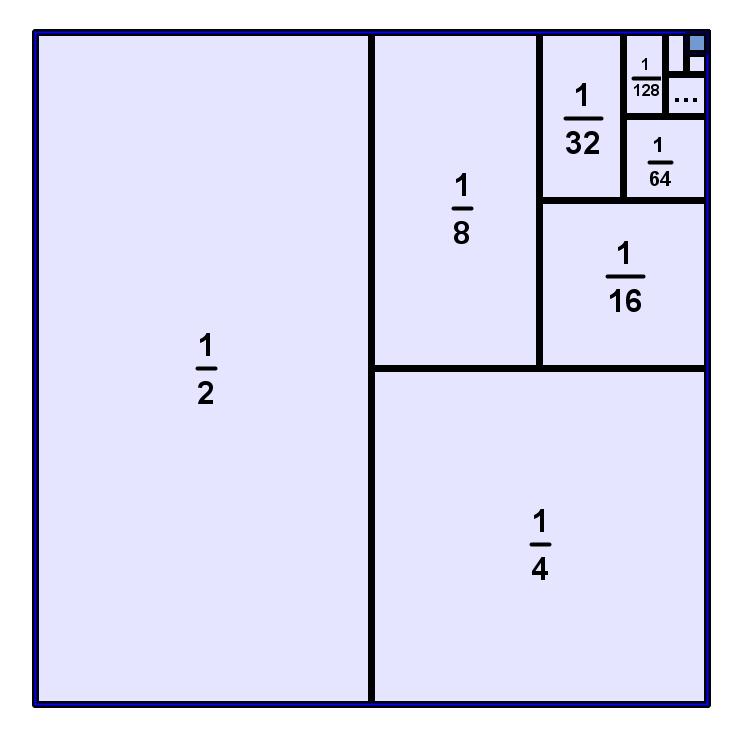
In a square of side length 1 (and therefore, area 1), cut the square in half; then cut one half in half (that’s a quarter); now cut one of the quarters in half (that’s an eighth); and so on and so on and so on (this puts the infinite in infinite sum). Eventually you’ll fill up the whole square! So this is a demonstration of the following amazing, and somewhat counterintuitive, fact that
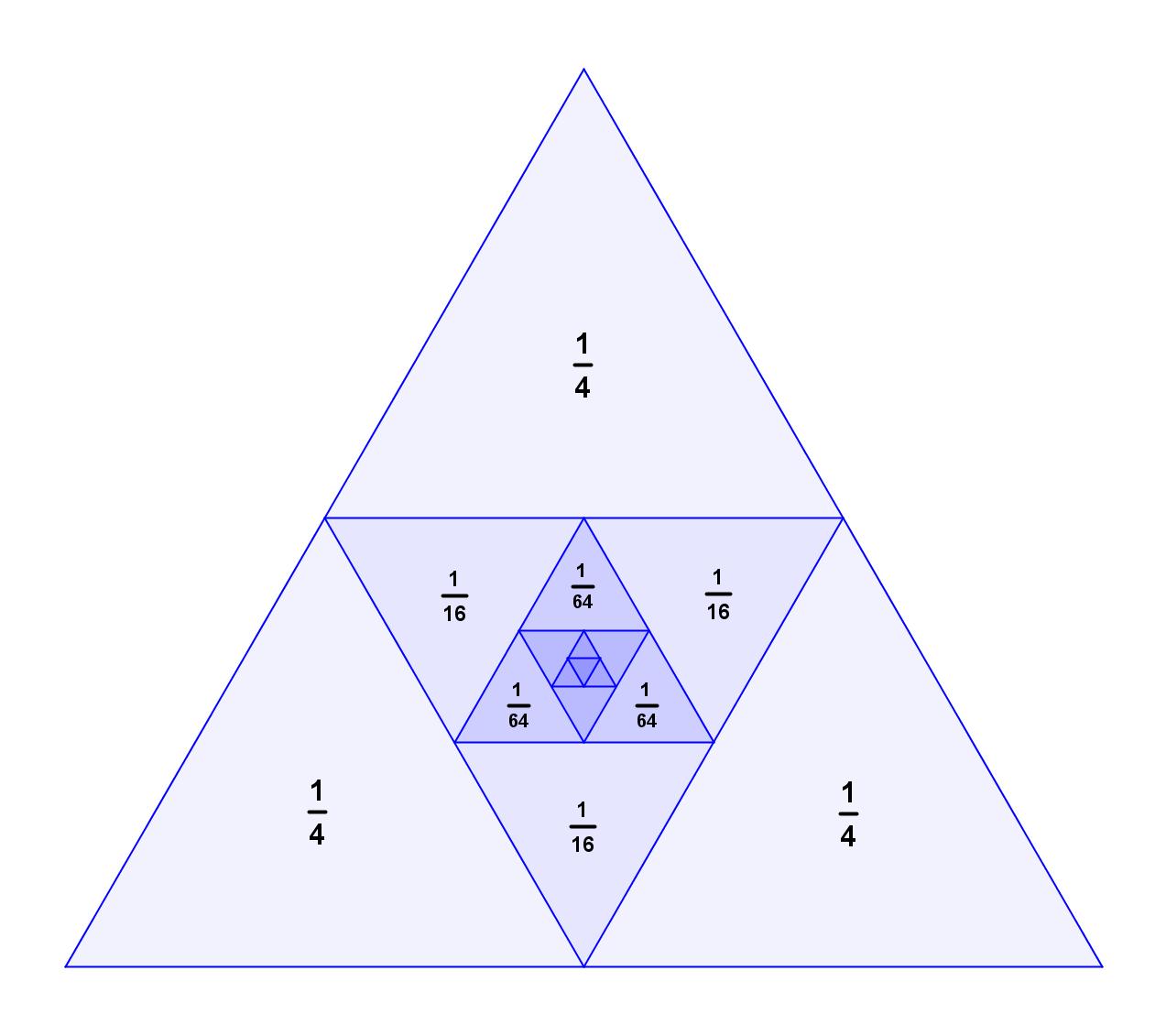
Similarly, this diagram
is a visual representation of the following sum:
As any good, lazy mathematician would say, the details are left to the reader.
Related Posts
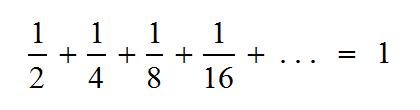
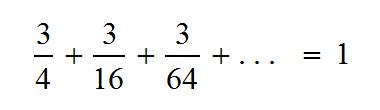
6 Comments
Rick · November 30, 2011 at 12:46 am
The sum below is equivalent to the square one:
3/4 + 3/16 + 3/64 + … =
(1/2 + 1/4) + (1/8 + 1/16) + (1/32 + 1/64) …
MrHonner · November 30, 2011 at 2:00 pm
Cool! I wonder if that equivalence could be visualized in an elegant way.
Taylor · December 27, 2012 at 3:42 pm
“I wonder if that equivalence could be visualized in an elegant way.” Ever the teacher, Mr. Honner.
MrHonner · December 31, 2012 at 11:51 am
I learned long ago that continually asking questions is a great way to deflect attention!
Quinn Culver · May 5, 2013 at 12:39 pm
Hi,
I used one of these pictures here: http://math.stackexchange.com/questions/382295/prove-by-mathematical-induction-that-1-1-4-1-4n-4-3/382302#382302. I found it via a google search. Please let me know if that’s not okay.
Quinn
MrHonner · May 5, 2013 at 9:09 pm
It’s fine, and I appreciate you letting me know, Quinn.