Well, it’s sort of natural. If nothing else, it demonstrates nature’s desire for symmetry.
Resources
More Free E-Books
Here’s another nice collection of free e-books on a wide range of topics.
http://www.e-booksdirectory.com/
The site has over 5,000 free e-books in subjects from Art, Computer Science, and Engineering. And the selections currently include about one thousand math e-books!
Appreciation Art
Magnetic Liquid Sculpture
Every now and then you see something on the internet that leaves you dumbfounded.
Like this video of Magnetic Liquid Sculpture.
http://www.youtube.com/watch?v=d44LW6KZ_iU
I honestly don’t even really understand what I’m looking at. But it’s amazing.
Data Resources Statistics
Rotten Tomato Analysis
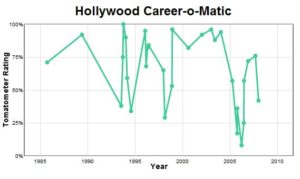This is a cool collection of data analysis from Slate.com that uses scores from the movie review site RottenTomatoes.com to chart the careers of actors and directors.
http://www.slate.com/id/2296070/
In addition to comparing the average career trajectories of actors and directors (a curious result!) and provoking interesting questions like “Why does the average rating seem to be falling over time?”, Slate provides a great little toy to play with: the Hollywood Career-o-Matic.
Type the name of any actor or director into the Career-o-Matic and see a quantitative overview of that person’s film history graphed out in front of you! You can even type multiple names and compare graphs! Scrolls over the highs (and lows) to get film details.
A nice little data tool, and it’s easy to see some fun, informal data projects coming from this. And it looks like it all started with this brilliant critique of M. Night Shyamalan.
Geometry
(Half) Parabola in Nature
I have a nice watering can with a long, straight spout. It’s good for watering tiny plants in hard-to-reach places.
It occurred to me that if I held the can so that the long spout were parallel to the ground, the water would probably come out in a parabolic path. The running water would have a horizontal velocity component, and the vertical component due to gravity would create the parabola
So I took some pictures.
And after playing around with Geogebra for a bit, I had my parabola!
This isn’t quite as pretty as this parabola in nature, but it’s more parabolic than these water spouts at the Detroit Airport.