Having spent a great deal of time dissecting and analyzing the 2011 New York Math Regents Exams, I was quite interested to see the January 2012 tests.
The same kinds of issues are generally present. There are instances of mathematical errors, poorly constructed questions, underrepresented topics, and 9th-grade questions on 11th-grade exams. Here is a quick overview of the Algebra 2 / Trigonometry Regents, the highest-level state math exam in New York.
Mathematical Errors / Poorly Constructed Questions
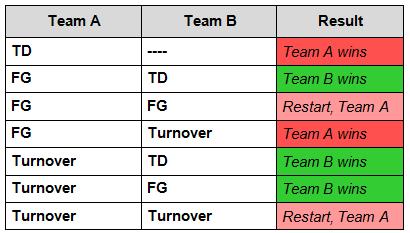
The exam writers for the New York Regents exams continue to find new and innovative ways to construct erroneous questions. Here is number 23 from the multiple choice section:
Which calculator output shows the strongest linear relationship between x and y?
 This is a bad question to begin with, in that it really isn’t a math question. The student isn’t being asked to ponder anything mathematical; instead, the student must recognize a step in an artificial procedure about which they have no real mathematical understanding. (The mathematical technique for finding linear regression equations is not taught in this course; it is expected that the student will use the calculator to generate the equation).
This is a bad question to begin with, in that it really isn’t a math question. The student isn’t being asked to ponder anything mathematical; instead, the student must recognize a step in an artificial procedure about which they have no real mathematical understanding. (The mathematical technique for finding linear regression equations is not taught in this course; it is expected that the student will use the calculator to generate the equation).
What’s remarkable here lies in the “answer”. The way you assess the relative strengths of regression equations is by comparing their correlation coefficients (the r values). Generally speaking, the closer r is to 1 or -1, the stronger the correlation. In answer choice (4), the value of r is closer to -1 than, say, the value of r is to 1 in answer choice (1). Thus, (4) is the correct answer. Pretty easy, right?
Amazingly, the situation represented in answer choice (4) is a logical impossibility. Since the r value is negative, this means the correlation between the two sets of data is negative; but the regression line’s slope (the b value) is positive! This cannot happen.
As a result, a scoring correction was issued (after the exams had most likely been graded) and all students were to be given credit for this problem regardless of what answer they put. And so another flawed question makes it through the draft-revision-publish cycle and into the hands of thousands of students.
Underrepresented Topics
By my count, only one question on this exam (worth 2 out of 87 total points) required the use of either the Law of Sines or the Law of Cosines. Now, I don’t know how many points should be allocated for these particular techniques, but they are fundamental ideas in trigonometry: they should be a non-trivial part of the course.
Indeed, a quick look at the exam’s reference sheet is illuminating: less than half the formulas that are traditionally provided for the student relate to questions on this particular test.
9th Grade Questions on 11th Grade Exams
The final question, and the highest-valued question (6 points) on this Algebra 2 / Trigonometry exam, asked the student to simplify the following expression:
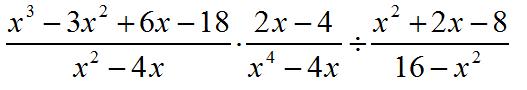 Once again we see a problem from the 9th-grade Algebra curriculum playing a significant role in the 11th-grade Math Regents exam. A quick look at the official Integrated Algebra Pacing Guide shows that dividing and simplifying rational expressions, the techniques that this problem requires, are part of the 9th-grade course.
Once again we see a problem from the 9th-grade Algebra curriculum playing a significant role in the 11th-grade Math Regents exam. A quick look at the official Integrated Algebra Pacing Guide shows that dividing and simplifying rational expressions, the techniques that this problem requires, are part of the 9th-grade course.
This isn’t necessarily an easy problem, and it does require dealing with a cubic polynomial (although factoring by grouping is an optional part of the 9th-grade curriculum). But this is yet another example in the evolution of this exam showing that, year after year, the hardest questions seem to get easier.
To be completely fair, it was nice to see the exam writers include asymptotes on their graphs this time (to avoid fake asymptotes like these), and they did demonstrate a little more understanding about 1-1 functions (perhaps they did a little studying after this disaster). But overall, it seems to be business as usual.