patrick honner

Math teacher in Brooklyn, New York

The Perfect Parallelepiped

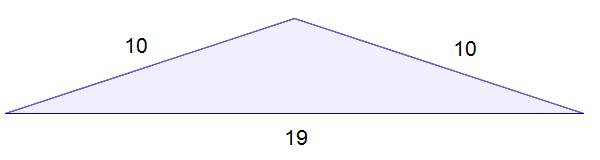
In general, it’s unusual for a rectangle to have sides and diagonals whose lengths are all integers (i.e., whole numbers).  Consider the following three rectangles, all of width 3:

diagonals

Looking at the different lengths, we see one place where the diagonal length is an integer, but in the other cases, the diagonal length happens to be a non-terminating, non-repeating decimal (i.e., irrational).  Indeed, the diagonal length will be an integer exactly when the length and width are part of a Pythagorean triple, but compared to the alternative, this is uncommon.  (While there are infinitely many occurrences of this, we can still meaningfully consider it uncommon).

Now, imagine the situation in three dimensions.  A rectangular prism (think of a cardboard box) has 12 sides, 12 face diagonals, and four space diagonals.  It would be extremely unusual for all of those 28 lengths to be integers.  Even if we didn’t limit ourselves to rectangular prisms, but we allowed for the box to be slanted in all directions (that is, a parallelepiped), it would still be a numerical miracle for all those lengths to be integers.

Well, meet the perfect parallelepiped!

a perfect parallelepiped

This was discovered by a couple of mathematicians at Lafayette College in Pennsylvania, using brute-force computer trials.  It looks like they found some others, too.   So thank you, Clifford Reiter and Jorge Sawyer, for giving me an extra credit problem for my next exam!

Related Posts

By patrick honner, ago

Benford’s Law

Benfords LawThis is an article about the discovery of new sets of data that seem to obey Benford’s Law–a curious mathematical characteristic of the numbers we collect from the world that is really more conjecture than law.

http://www.newscientist.com/article/mg20827824.700-curious-mathematical-law-is-rife-in-nature.html

It seems that in scores of data sets collected from natural phenomena, the numbers we see tend to start with the digit 1 far more often than, say, with the digit 6.  Indeed, statistical analysis shows that when you look at population numbers, death rates, street addresses, lengths of rivers, stock prices, and more recently, depths of earthquakes and brightness of gamma rays, the observed numbers start with the digit 1 about 30% of the time.  The occurences of other digits as the leading digit fall as you go up the scale.

Apart from being a natural curiosity, Benford’s Law has proven to have some very useful applications.  Scientists can use Benford’s Law to help predict phenomena and look for trends in data, as the rule gives number-crunchers an idea of what they might be looking at from the start.

Additionally, Benford’s Law has been successfully used to identify all kinds of numerical fraud–tax fraud, voter fraud–because when people are faking numbers, they tend to evenly distribute leading digits.  Benford’s Law tells the data-police that if approximately 1/9 of the numbers they are looking start with 1, then something fishy is going on.

Keep that in mind next April.

By patrick honner, ago

Math Lesson: Predicting the Vote

newspaperI am very excited to have my first Lesson Plan published by the New York Times Learning Network.  I wrote a mathematics lesson built around profiling the upcoming presidenital election, using data and analysis from Nate Silver’s 538 Blog at the Times.

The lesson is titled “Predicting the Vote: Analyzing Election Data”, and can be found here:

http://learning.blogs.nytimes.com/2010/10/18/predicting-the-vote-analyzing-election-data/

Trying to write a lesson plan for general use was much more challenging than I imagined, but it was an interesting and educational experience for me.  Hopefully it will produce some interesting educational experiences for others.

By patrick honner, ago

The Final Word in Triangle Appreciation

As has been previously noted, October has been a nice month for triangle appreciation.  Today, 10/19/10, offers us one more polygon to ponder.

Consider the 10-19-10 triangle.

10-19-10 triangle

It’s a fairly ordinary triangle, as triangles go.  It’s a little short compared to the other triangles we’ve looked at recently, but there’s nothing wrong with that.

What’s special about the 10-19-10 triangle is that it’s our last chance this month to enjoy triangularity.  Tomorrow, the Triangle Inequality steps in.  You can’t have a 10-20-10 triangle, because once the third side hits 20, you need all of the 10s to get from point A to point B.  There’s no wiggle room for the triangle’s interior.

10-20-10 Triangle

Although I must admit, I do find much to admire in this degenerate triangle.

Related Posts

 

By patrick honner, ago

The First Word Calculator

word calculatorThis is a pretty awesome widget from the folks at Wolfram Alpha:  a word calculator!

http://blog.wolframalpha.com/2010/10/15/celebrating-dictionary-day-with-new-word-data/

It does the basic things you’d expect, like give you definitions, pronunciations, synonyms, and the like.  But it also gives you cool things like word frequency (“frequency” is the 3209th most common word) and hyphenations (me-di-e-val has 8 letters and 4 syllables)

And, when I typed my name in, I learned that 599,125 people are named Patrick, and our most common age is 46.

WolframAlpha’s mission is to make the world’s information computable–not just searchable.   I guess the lesson here is that everything is computable in some way.

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: