Mr Honner

Application Geometry Technology

Water Ellipses?

A funny thing happened on the way to the graphing utility.

I thought I’d use Geogebra to estimate the equation of the water parabola I saw at the Detroit Airport.

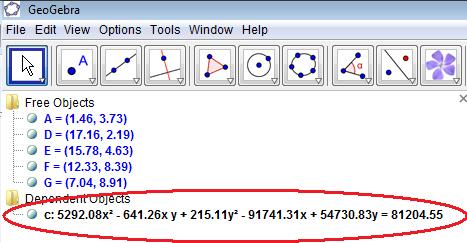
So I pasted the photo into Geogebra, dropped five points on the arc, and then used “Construct Conic Through Five Points”. The results are on the right.

Now the weird part: the equation is not a parabola, but an ellipse. I thought that perhaps I had done a poor job of selecting points, but no matter how I chose the points, the equation came up as an ellipse.

Note the presence of both an x² and a y² in the equation below.

Is this a limitation of Geogebra? Is this an anomaly caused by rendering the digital picture? Or is the assumption that the path of the water is parabolic faulty?

Application Geometry

Water Parabolas

It’s not easy to see, but at the right is a picture of the famous water parabolas at the Detroit Airport. The parabola certainly is a favorite among the fountain designer. I wonder why?

Upon closer inspection, I’m not sure it’s a parabola! Check out my attempt to find the equation of this parabola using Geogebra.

And here is a lovely video of the water feature in action: http://www.youtube.com/watch?v=VSUKNxVXE4E

By patrick honner, 14 years11 years ago

History Statistics

David Blackwell

David Blackwell was a highly-regarded statistician and mathematician who taught at UC Berkeley for 30 years. Apparently he was the kind of mathematician who could become interested in a new topic, learn about it, and then quickly produce profound results. Then he’d move on. Blackwell died on July 8th: his obituary in the NYT can be found here.

Among other things, Blackwell was a strong proponent of the Bayesian approach to statistical inference, and he produced results in Game Theory regarding bluffing and dueling.

By patrick honner, 14 years11 years ago

Application Appreciation

On Flyswatters

Designing a flyswatter is an interesting exercise in optimization.

You want it have enough holes so that it can quickly achieve swatting speed, but you don’t want it to have so many holes as to substantially decrease the chance of actually making contact with the pest.

I wonder if there is an industry standard for a flyswatter’s empty-space-to-surface-area ratio.

By patrick honner, 14 years11 years ago

Economics

Measuring Mortgage Defaults

According to a recent study the default rates for mortgages over one million dollars is nearly twice as high as the default rate for mortgages under one millions dollars (14.3% to 8.3%). A default on a mortgage essentially means that the home-owner stops making mortgage payments and the bank takes possession of the home.

There are a lot of interesting mathematical, sociological, and perhaps ethical questions here, but I wanted to point out that although the above probabilities are interesting, the number and total value of the mortgages in question are probably more relevant data to consider.

For example, if only 1/10 of all mortgages are over a million dollars, then this statistic might not be that important; on the other hand, if a good number of defaults are way over a million dollars, than this statistic isn’t telling the real story either, but in a different way.

As an aside, renting vs. owning is a general and interesting mathematical question to explore in a variety of different contexts.

By patrick honner, 14 years11 years ago

Follow Mr Honner