Water Ellipses?
A funny thing happened on the way to the graphing utility.
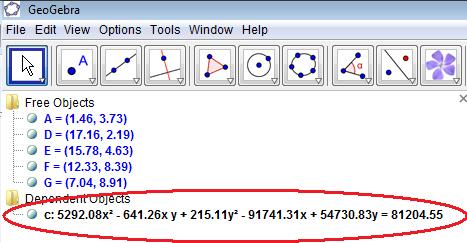
I thought I’d use Geogebra to estimate the equation of the water parabola I saw at the Detroit Airport.
So I pasted the photo into Geogebra, dropped five points on the arc, and then used “Construct Conic Through Five Points”. The results are on the right.
Now the weird part: the equation is not a parabola, but an ellipse. I thought that perhaps I had done a poor job of selecting points, but no matter how I chose the points, the equation came up as an ellipse.
Note the presence of both an x² and a y² in the equation below.
Is this a limitation of Geogebra? Is this an anomaly caused by rendering the digital picture? Or is the assumption that the path of the water is parabolic faulty?
Related Posts

44 Comments
dhc · July 22, 2010 at 10:54 am
Water does travel differently in air than solid objects, but not that much different.
mrhonner · July 22, 2010 at 6:23 pm
So what are the differences?
Whit Ford · July 23, 2010 at 4:41 pm
Try plotting three points in geogebra, then solve for the three coefficients of the corresponding quadratic manually. Plot the resulting equation on the same image and see where it differs from the photograph of the water stream.
Perhaps some combination of air resistance and the surface tension of the water stream conspire to produce a shape that is more elliptical than parabolic.
Emily VA · June 14, 2011 at 9:23 am
Fascinating! I’ve been using videos and pictures of that fountain to motivate parabolas without even stopping to question it.
MrHonner · June 14, 2011 at 12:29 pm
I get the feeling that any half-ellipse can be decently approximated by a well-chosen parabola. So maybe this isn’t really that surprising.
Samuelson Mathxp · June 14, 2011 at 12:48 pm
Could the velocity at which the water is being projected throw off the eccentricity to that of an ellipse?
MrHonner · June 14, 2011 at 12:56 pm
If it was a ball being projected, we’d expect a parabola, regardless of the velocity. I guess that’s where I’m starting in my informal analysis of the situation. If something is indeed changing the parabolic path to an elliptical one, I’d be more inclined to look at some characteristic of the water (like surface tension, as Whit Ford suggested).
Of course, the water can’t complete a full ellipse, as it will crash into the ground. So it’s really only the top of an ellipse. And maybe tops of ellipses aren’t any different from parabolas?
Samuelson Mathxp · June 14, 2011 at 1:15 pm
……that is very true. I was thinking that the short span travelled by the water may not give gravity enough time to reflect its true properties on a fast moving stream.
Christopher Danielson · January 15, 2013 at 7:00 am
It seems important that the major axis of your ellipse appears not to be vertical. But I have run no calculations on the provided formula. Because I am lazy.
MrHonner · January 15, 2013 at 12:11 pm
I agree that it’s worth noting that the axes are not vertical/horizontal, but in the end, does it really make a difference? We can rotate graphs without changing their nature.
l hodge · January 15, 2013 at 8:29 am
Once you let go of a ball, you personally are no longer acting on it. After the pump pushes out a particle of water, is the particle still being acted on by the pump via the solid arc of water from the pump to that original particle? When the pump pushes another particle forward, does that particle then “bump” into the one infront and so forth?
MrHonner · January 15, 2013 at 12:15 pm
Sounds like you are headed toward some sort of wave/particle duality of water streams theory.
l hodge · January 15, 2013 at 9:08 pm
Yah, yah, your right, that doesn’t make any sense at all.
Nice call, Chris, on the rotation. Rotating the image in geogebra allows for a pretty good fit with a parabola.
Will least squares cubic regression on any five points that are not a perfect parabola ever produce a quadratic? Similar issue here I think – more degrees of freedom with an ellipse.
Interesting question. Ever investigate something like this (affect of rotation, tilt, or optix on a curve) with a class? I don’t know anything about camera optix, but rotation & tilt seems doable given physical models for the curves, strong light to make a shadow, and a few days of time.
MrHonner · January 16, 2013 at 8:10 am
I’ve never done this with a class, but this conversation certainly has produced a lot of great project ideas. Someone on Google+ was talking about how this may be related to the pincushion effect of camera lenses, and how programs that stitch photos together to create panoramas need to navigate the issue. Fascinating stuff.
https://plus.google.com/u/0/117272697671979968695/posts/WkrECfP8qLt
l hodge · January 15, 2013 at 9:02 am
Interesting and easy to see how well/poorly a parabola can fit an ellipse(or circle)using Desmos with sliders. Which sort of ellipse is best approximated by a parabola?
MrHonner · January 15, 2013 at 12:14 pm
It’s interesting that you bring up the question of how well you can fit a parabola to an ellipse, because we were debating that issue in the comments of “This is Not a Trig Function”:
Francisco · January 15, 2013 at 12:06 pm
It is a parabola indeed, but you can only see it as such if your camera is perfectly aligned with (parallel to) the plane in which it is contained. Otherwise, your camera will register “other curves.” Think about it. If you place yourself on top of it and take a pic, you will see just a segment, right?
MrHonner · January 15, 2013 at 12:20 pm
That’s an interesting point. This might explain why it doesn’t register as a parabola, but does it explain why it registers as an ellipse?
Your point also gets me wondering about whether tilted parabolas could still be parabolas. Say your camera resided in the perpendicualr bisector of a given parabola. If the camera were pointed normal to the plane of the parabola, you’d see a parabola; but what if the camera were pointed slightly “up”? You’d see something parabola-like. Would it still be a parabola, I wonder.
Francisco · January 15, 2013 at 1:03 pm
You still have to account for distortions produced by the optics of your camera, of course.
MrHonner · January 15, 2013 at 2:02 pm
In this case, I’ll be taking all pictures with my theoretical camera.
Francisco · January 15, 2013 at 2:25 pm
🙂
johnr · January 15, 2013 at 1:19 pm
The conic sections are slices of cones. If the plane of the camera frame is parallel to the direction of the cone from hich the parabola came then it ought to show up as a parabola.
If you tip the plane on one direction you ought to get an ellipse, in the other direction a hyperbola.
Air resistance might modify this slightly, but probably not much at these velocities.
Francisco · January 15, 2013 at 1:39 pm
Not sure that is true. The “slice of the cone” is never modified by the optics. You always have a parabola no matter what (in ideal conditions), but your optics tilt it and make certain areas of the curve to appear closer than what they really are—the farther from the center, the bigger the distortion.
A different issue arises when you realize that this otherwise ideal parabola lives in a tree-dimensional space, and each particle is subject to the effect of a vector field. I agree that the physical distortions due to air flows/resistances should not affect the curve too much, though.
Vince · January 15, 2013 at 1:04 pm
That’s very cool and the conversation subsequently has been a great read. Interesting point about the angle of photography!
Imre Polik · January 15, 2013 at 1:39 pm
The parabola is a transition between an ellipse and a hyperbola. It is a zero measure object between the two. A quadratic curve chosen at random is a parabola with probability 0. So it is not surprising that the curve you got is not a parabola. It’d be suprising if you got a perfect parabolic equation.
Factors like wind resistance, surface tension, friction, optics are all against the parabola.
On the other hand, I’m not sure that the curve is a parabola in theory at all.
MrHonner · January 15, 2013 at 2:07 pm
Interesting point about the parabola as transitional object. I’d never really thought that, in the space of quadratic curves, ellipses might be more likely than parabolas. Cool idea!
That being said, as you point out, whether it should be a parabola or not is interesting to ponder as well.
Fergus · January 15, 2013 at 6:45 pm
I found this on twitter this morning. It intrigued me and I have hastily done some psuedo-maths, scribbled on an old envelope, but I’ve got to get to work. I will look into it some more when I get home tonight. Ignoring air resistance etc (which I am pretty certain you could do over this small distance) I am quite sure it is the angle of the camera that is causing this.
I picked 5 points on a perfect parabola and then tilted the plane of the parabola by 10 degrees. This changed the apparent height of the points when viewed from a position 2 metres from, and perpendicular to the original parabola. The new, apparent heights of the points produced an ellipse in geogebra.
MrHonner · January 16, 2013 at 8:06 am
Did you do this experiment virtually, or did you create a physical model and take pictures? It sounds cool–you should post and share.
Sean Wilkinson · January 15, 2013 at 10:19 pm
I’m with Imre. I think the wind resistance people might be onto something, but I’m not sure we even need that. The coefficient on y^2 is so small (compared to the one on x^2) that it seemed to me to be within the range of error. I downloaded the picture and tried to replicate your result. With 5 tests (using a new set of 5 points each time) I got the following coefficients on x^2 (rounded to the nearest 1):
-57
-52
0
-47
-35
Whereas the coefficients on x^2 were always way into the thousands.
(Also, it’s interesting that your coefficient on y^2 is so much higher than my average. We must have different point-clicking biases (or maybe different types of computer monitor…)
MrHonner · January 16, 2013 at 8:17 am
Interesting. So basically the idea is that a small error in locating the points may indeed spoil the perfect parabola, but perhaps we can quantify a margin of error and see if the coefficient of y^2 falls within it. Sounds like a total differntial problem, with a mix of statistics! Cool.
PhilH · January 15, 2013 at 10:24 pm
Just passing through and noticed no one had mentioned the special nozzles and pumps/cannons used to produce these streams. I can vaguely remember a show about them some years ago. It has something to do with aligning water molecules in the stream I believe. I can’t even remember what the whole setup was called. I wonder if that might have anything to do with how the water behaves. I do remember that it caused the water to make the full arc where water would normally break up into drops. It also caused a lot less splash as it landed.
MrHonner · January 16, 2013 at 8:13 am
Thanks for crossing over from Google+ to comment, Phil! It almost sounds like what you are describing is a kind of rifling of these nozzles; is that the gist of it?
If you happen to remember the show, please share! Or maybe I should just check the listings for “How It’s Made”.
johnr · January 16, 2013 at 9:07 am
I saw a “How It’s Made” on drinking fountains a few weeks ago.
Season 20 episode 4
http://en.wikipedia.org/wiki/List_of_How_It%27s_Made_episodes
l hodge · January 16, 2013 at 12:48 pm
Did not know that geogebra regression responds dynamically as you adjust the original regression points. It is very sensitive with regards to Imre’s comment.
How neat is it that you can plot some points & fit a curve, rotate those points and fit a curve again, and adjust the points and dynamically watch how the equation(s) change. The equation for a rotated parabola took me by surprise – thought it was the equation of an ellipse.
Paul Savoie · January 16, 2013 at 1:03 pm
Is there a dependence on the order in which points are selected? Based on the image, A is on the far left, and then you have D, E, F, G from right to left. If order of point selection matters, then an ellipse would give you the result you’re looking for (starting from point A and proceeding alphabetically), as the program is looking for an equation to connect A, D, E, F, and G in order. Of course, if you chose the points from right to left or left to right, and still got an ellipse, then the problem’s not so simple.
Never worked with the program myself, but a similar idea occurs in synthetic chemistry. For some reactions, the order in which you add the starting materials matters.
William Hanisch · January 16, 2013 at 3:26 pm
The conics can also be interpreted (defined) as projective images of circles. (If you look at a circular coin from an angle, you will see an ellipse. If you shine a flashlight onto a wall and tilt it, you can can get all the conic sections to appear on the wall.) Perhaps the angle from which you snapped the photo is projecting a parabola into an ellipse.
Imre Polik · January 16, 2013 at 3:35 pm
A parabola cannot be projected to an ellipse or a hyperbola for that matter. A projection cannot change the class of the quadratic curve. Digital cameras distort the images in other ways, so it is not really a projection, but rather something nonlinear.
In this case the curve is nearly a parabola, but only nearly. In practice it cannot really be _exactly_ a parabola.
I’d venture to say that in practice there are no parabolas or straight lines or circles. Even if you draw a perfect circle on the screen and put five points on it you won’t get the equation of the circle, you’ll have some (very small) noise added to it. I’ll probably be an ellipse.
William Hanisch · January 16, 2013 at 4:32 pm
Imre,
I’m not quite sure I understand your first paragraph.
A circle is certainly a quadric curve, and any conic section (an ellipse, parabola, or hyperbola)–which is also a quadratic curve–is the projection of a circle on a plane. (This is what a conic section means in projective geometry.) So, I’m not sure what you mean by “[a] projection cannot change the class of the quadratic curve.” The conics are all of the same projective class, and as such, one can be transformed into any other by a projection. So I also don’t understand why you state that “[a] parabola cannot be projected to an ellipse or a hyperbola for that matter.”
I do, of course, agree with you “that in practice there are no parabolas or straight lines or circles.” Those objects are in the world of mathematics, and not in the world of water and cameras and pencil marks and such.
William Hanisch · January 16, 2013 at 5:11 pm
Imre,
Here’s another way to look at what I’m trying to say:
Rather than a supposed perfect parabola suspended in space, we instead consider a supposed perfect circle on a table top. Now we try to photograph this supposed perfect circle as best we can. Unless we are directly and perfectly above the circle, the photo will appear to be that of a non-circle ellipse. That the photo shows an ellipse (but not a circle), it does not imply that the original object (the one we photographed) is not a circle.
What I’m trying to say is that the angle from which the photograph is taken will project the image. And any conic will be transformed into another conic by such a projection. That’s why I’m suggesting that the photograph can very well be that of an ellipse even if the object photographed is that of a parabola.
Imre Polik · January 16, 2013 at 5:39 pm
Ignore my reply about projection above, it only applies to the scenario when we take a picture.
A circle and an ellipse belong to the same class, both have two positive eigenvalues in their matrix.
You won’t be able to photograph a circle and end up with a parabola, no matter where you take the picture from.
Two concepts are washed together in some posts above: projecting from a point and taking a picture.
When we play with a flashlight near a wall we fix a point (bulb), take rays from this point through points of the object (opening of the flashlight) and take the intersection of these rays with a plane (wall) _beyond_ the object. Depending on the angle the image on the wall can be any quadratic shape.
When taking a picture with a camera the setup is similar, but there’s a crucial difference: the intersection of the rays and the plane is taken _between_ the object and the fixed point. This way a closed curve will always stay closed and the type of the curve will not change.
William Hanisch · January 16, 2013 at 6:57 pm
Imagine a large circle painted on the floor. Now step inside this circle, stand at various heights, and take photos of whatever part of the circumference you can see. Are you sure the curves of all your photos will be ellipses?
As a simple example of this, suppose that the circle, instead of being painted on the floor, is cut out of the floor, so that you can point the camera in the same plane as the floor. In this case, your photo will show a straight line, which certainly isn’t a closed curve.
l hodge · January 16, 2013 at 6:09 pm
This is the sort of thing I think might make an interesting lesson(s). Similarily, if you imagine a solid ramp next to a set of stairs the “bottom on the ground” is a rectangle and so is the “top” part you would walk on. But the top is a bigger rectangle. Now suppose the part of the ramp you walk on is a parabola or circle or ellipse, what is the bottom (the projected image)? You get some nice pythagorean theorem applications out of it and, to me, the shape of the bottoms of the ramps, or the ramps themselves is not obvious.
Alan Eliasen · September 24, 2013 at 10:00 pm
Imre Polik’s comments above are right on target. There is only one parabola, and it’s the infinitely-thin case where eccentricity of the conic section is exactly 1. From 0 to 1 is an ellipse, and greater than 1 is a hyperbola.
It should also be noted most strongly that you’d only expect to see a hyperbola if the earth was flat and gravity perpendicular to the earth’s surface. It’s not. We live on a sphere, so all other ballistic paths / orbits are actually sections of an ellipse! Kepler demonstrated this hundreds of years ago.
S. Weinstein · February 14, 2014 at 9:13 am
The trajectory of the water is an ellipse having one of the foci at the earth’s center. If you assume g is constant then you get a parabola. Bottom line, over the visible part of this water stream orbit, the parabola and ellipse are indistinguishable.