August 2012

Here is another installment from my review of the June 2012 New York State Math Regents exams.

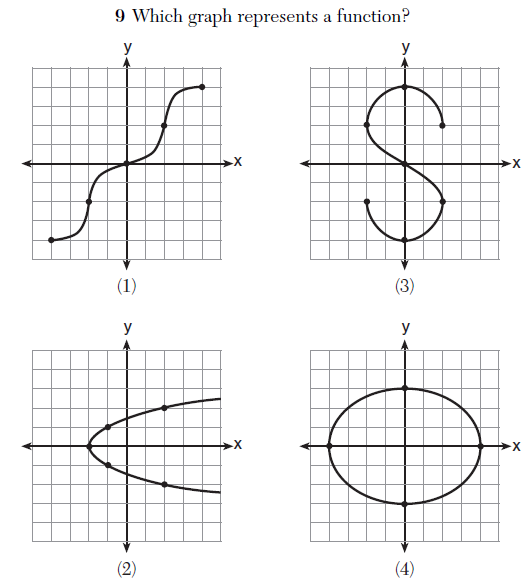
Below is a problem from the Integrated Algebra exam.  Which of these graphs represents a function?

Have you identified the function?  Well, you’re right, because all of these graphs could represent functions!

What the question presumably intends to ask is “Which of these graphs represents y as a function of x?”  Under this interpretation, the correct answer is (1).  But in (2), we see a graph that represents x as a function of y.  So it, too, represents a function.

Indeed, even graphs (3) and (4) could represent parametric functions.  For example, (4) could be written.

This plane curve is a function of t.

I doubt this makes much practical difference in the outcomes on this exam, but precision is important in mathematics; it should be modeled for students on official assessments.  And those writing these important exams should be familiar enough with the content to write precise and accurate questions.

Here is another installment from my review of the June 2012 New York State Math Regents exams.

Below is a problem from the Integrated Algebra exam that highlights the artificiality of so-called “real world” problems.

In order to solve this problem in a high school algebra class, a crucial assumption must be made, namely, that every point on the target is equally likely to be hit.  This means that the dart is just as likely to hit a spot near the bulls-eye as any spot near the edge.

Math teachers end up spending a lot of time training students to make these assumptions, probably without ever really talking explicitly about them.  It’s not necessarily bad that we make such assumptions:  refining and simplifying problems so they can be more easily analyzed is a crucial part of mathematical modeling and problem solving.

What’s unfortunate is that, in practice, students are kept outside this decision-making process:  how and why we make such assumptions isn’t emphasized, which is a shame, because exploring such assumptions is a fundamental mathematical process.

Is it a reasonable assumption that every point is equally likely to be hit?  Well, if the thrower is skilled, the dart is probably more likely to land near the bulls-eye.  Would gravity make the lower-half more likely than the upper half?  Discussing these, and other relevant factors as part of the modelling process can be engaging, fun, and highly mathematical.

But when standardized tests with “real world” problems are the focus of education,  students usually end up getting trained to not ask these questions.

Here is another installment from my review of the June 2012 New York State Math Regents exams.

On the left is a problem from the Algebra 2 / Trigonometry exam; on the right, a problem from the Geometry exam.

Notice that no scale is indicated on any of the graphs here.  That is, there is no indication of what “one unit” is equivalent to on any graph.

I admit that I’m pretty sloppy when it comes to labeling graphs, however I know some teachers make accurate labeling and scaling a point of emphasis when it comes to creating graphs.  Properly understanding the scale of a graph can be of crucial importance, especially when trying to with questions pertaining to specific numeric values, as in these above.

Tests should stand as models of mathematical content and practice for students; they should not reinforce bad mathematical habits, like ignoring scale.

I know very little about early childhood education, but have recently started to think more about it.  I greatly enjoy interacting intellectually with my nieces and nephews and find it fascinating to explore ideas like fractals, infinity, and ordering with them.  But I don’t really know anything about the theory of how children learn, what they should learn, or when they should learn, mathematically, or otherwise.

To begin exploring the idea, I thought about possible fundamental questions and eventually settled on this:  What are some important content-independent skills that children need to learn?

I posted the question on Google+, and Don Pata, MrBombastic, Jim Wilder, and Christopher Danielson all offered some great ideas.  Here’s the list we compiled through discussion, in no particular order.

Problem-Solving Perseverance — the ability to sustain focus and work through a problem to the end

Intellectual Discipline — the willingness to focus and invest energy on learning and development

Number Sense — an intuitive understanding of quantity:  magnitudes, relationships, and scales

Reflection — the ability to objectively self-assess, refine, and adapt

Communication — the ability to express information and emotion in a variety of ways, and appropriately interpret and process the expressions of others

Courage —  the willingness to fail

Curiosity — the habit of inquisitiveness and the ability to ask good questions

A good list to start with!  Thanks for all the help, and if there are other suggestions, please feel free to leave them in the comments.

You can see the original thread on Google+ here.