Regents Recap — June 2012: Spot the Function

Published by patrick honner on August 22, 2012August 22, 2012

Here is another installment from my review of the June 2012 New York State Math Regents exams.

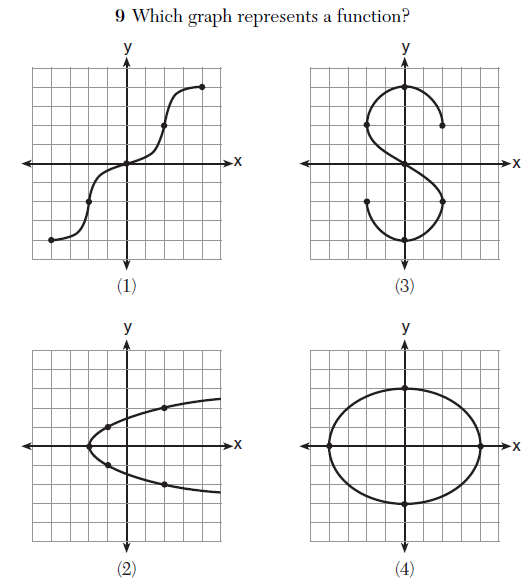
Below is a problem from the Integrated Algebra exam. Which of these graphs represents a function?

Have you identified the function? Well, you’re right, because all of these graphs could represent functions!

What the question presumably intends to ask is “Which of these graphs represents y as a function of x?” Under this interpretation, the correct answer is (1). But in (2), we see a graph that represents x as a function of y. So it, too, represents a function.

Indeed, even graphs (3) and (4) could represent parametric functions. For example, (4) could be written.

$r(t) = < 4 \thinspace cos(t) , 3 \thinspace sin(t) > , 0 \le t < 2\pi$

This plane curve is a function of t.

I doubt this makes much practical difference in the outcomes on this exam, but precision is important in mathematics; it should be modeled for students on official assessments. And those writing these important exams should be familiar enough with the content to write precise and accurate questions.

Categories: Teaching

patrick honner

Math teacher in Brooklyn, New York

7 Comments

@manmathmo · August 24, 2012 at 5:37 am

Hey, just wanted to point out that I was taught at university (and sixth form I think) that 2, 3 and 4 are not functions! They are not well-defined. Further reading on this from Fields Medallist Tim Gowers here: http://gowers.wordpress.com/2009/06/08/why-arent-all-functions-well-defined/

MrHonner · August 24, 2012 at 7:28 am

It is clear that y is not a function of x in the graphs of (2), (3), and (4), but that doesn’t mean those graphs could not represent functions. The graph of (2) seems to be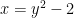 $x = y^2 - 2$ , and thus could rightly be considered the graph of the function $g(y) = y^2 - 2$ .

Sir Tim’s blog post is about functions that aren’t well-defined (which means the “function” doesn’t yield the same output for equivalent representations of an input); I don’t think it has anything to do with these functions, which are well-defined.

@manmathmo · August 24, 2012 at 8:04 am

He actually cites (a translation of) (2) as a gunction, the article does address the same issue as the question.

However, reading your post more carefully, I see the point you’re making. I’m not sure I agree with it though. Any competent mathematician can see what they’re getting at here, and isn’t part of being a good mathematician being able to interpret slightly vague questions sensibly? After all, in this question x and y are labelled on the axes, so they must be asking about one or the other. The question doesn’t work if you consider functions of y, so you must have to consider functions of x (alternatively you get the idea from the way they’ve presented the graphs!).

I’m not familiar with these exams, and it does look like they have a track record of being sloppy. But I do think vagueness is sometimes a pretty good test.

MrHonner · August 24, 2012 at 8:42 am

Gowers refers to $g(x) = \pm \sqrt(x)$ as a “gunction” (it’s easier to just call it a relation), but notice it’s a “gunction” of x. If we instead choose to think of x as dependent on y, then (2) is indeed the graph of a function.

I understand that these criticisms may seem pedantic to those outside the worlds of public schools and standardized exams, but these exams are becoming the de facto focus of schooling.

The larger point I’m trying to make is that students, teachers, and schools are now all evaluated on test performance, and these tests are sloppy, erroneous, and often reinforce misunderstanding.

Students shouldn’t have to guess what the exam-writer has in mind, and my career as a math teacher shouldn’t depend on how my students perform on a test that’s constructed by someone who doesn’t really understand what a function is (for a much worse example, see this).

@manmathmo · August 24, 2012 at 9:34 am

Yes, I agree, but I still think this particular question gives enough information, even though it’s given visually rather than in prose, to get the benefit of the doubt.

I also feel uncomfortable with increasing focus on testing, especially when it appears the grading is very politically influenced as we have in the UK.

All I’m really saying is that I wouldn’t characterise this question considered in isolation as asking you to guess what the examiner is thinking – enough information is given and it is clear enough for someone who understands the material like you or I. I don’t think we should aim for exams that are absolutely crystal clear and precise about what is required. The ability to analyse a question, consider why it has been asked and produce an appropriate answer seems like an important high level skill to me (it’s part of the Cambridge maths tripos although obviously that’s a very different kind of exam).

I do agree that that inverse example you linked to is egregious, so I guess the context tips in favour of your analysis, that they don’t really know exactly what they’re doing or there isn’t enough oversight. Don’t write off questions just because they’re vague though!

MrHonner · August 24, 2012 at 9:56 am

We don’t disagree about the value of vague questions: learning how to navigate the inexactness of the real world is what mathematical modeling is all about, and it’s an essential skill for students to develop.

And I also agree that most students won’t be troubled by this problem.

But I disagree with your claim that “enough information is given”. It isn’t. Just because x is the horizontal axis does not mean it automatically is to be considered the independent variable. The plane curve, r(t), given above, is unequivocally a function (of t). It doesn’t matter that its graph does not represent y as a function of x.

I think your real claim is “Given the context of secondary mathematics classes and standardized tests, a knowledgeable test-taker can likely fill-in the assumptions that the exam-writer is making in order to give the answer that is anticipated”.

This is a far different claim. And as it pertains to the larger point I’m making, I don’t think the fact that it may be true here really matters.

@manmathmo · August 24, 2012 at 10:22 am

Sure, the rights and wrongs of this particular question pale into insignificance compared to the discussion over the role of standardised testing on which we probably agree. Still a worthwhile discussion though, given how important questions are in a maths lesson.

I really think the parametric thing is a red herring here, the x and y variables labelled on the axes tell you explicitly that those are what we ought to be thinking about, even though they aren’t mentioned in the prose of the question. A picture’s worth a thousand words, after all. I’m interested to know, would the question still be too unclear in your opinion if the prose were the same but the axes were labelled x and f(x)? Also, unlike in the inverse question you linked, if you interpret this question as intended then the answer is not incorrect, and I do think that makes a difference.

I think I would also claim the question isn’t misleading or confusing, although it might a bad view of functions, particularly in the context of this exam’s history of poor questions. I guess I agree that as this question fits into the bigger picture, it’s pretty bad.