Regents Recap — June 2012: Throwing Darts

Here is another installment from my review of the June 2012 New York State Math Regents exams.

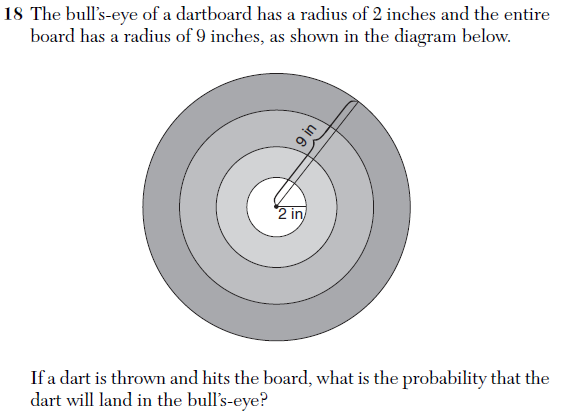
Below is a problem from the Integrated Algebra exam that highlights the artificiality of so-called “real world” problems.

In order to solve this problem in a high school algebra class, a crucial assumption must be made, namely, that every point on the target is equally likely to be hit.  This means that the dart is just as likely to hit a spot near the bulls-eye as any spot near the edge.

Math teachers end up spending a lot of time training students to make these assumptions, probably without ever really talking explicitly about them.  It’s not necessarily bad that we make such assumptions:  refining and simplifying problems so they can be more easily analyzed is a crucial part of mathematical modeling and problem solving.

What’s unfortunate is that, in practice, students are kept outside this decision-making process:  how and why we make such assumptions isn’t emphasized, which is a shame, because exploring such assumptions is a fundamental mathematical process.

Is it a reasonable assumption that every point is equally likely to be hit?  Well, if the thrower is skilled, the dart is probably more likely to land near the bulls-eye.  Would gravity make the lower-half more likely than the upper half?  Discussing these, and other relevant factors as part of the modelling process can be engaging, fun, and highly mathematical.

But when standardized tests with “real world” problems are the focus of education,  students usually end up getting trained to not ask these questions.