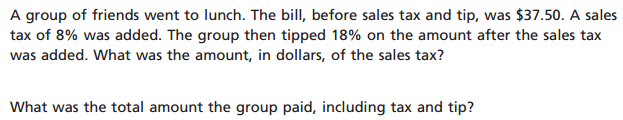This is the second part of a conversation with Grant Wiggins about rigor in mathematics, testing, and the new Common Core standards. You can read Part 1 here.
Patrick Honner Begins
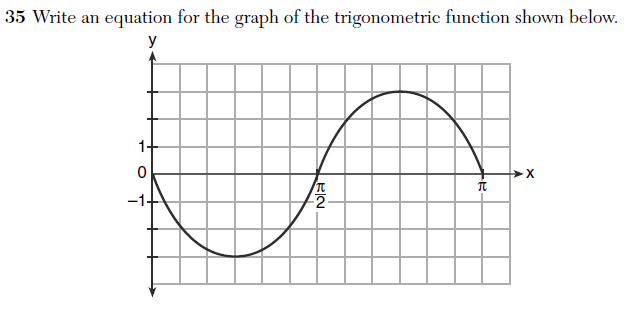
One thing I realized during Part 1 is that I need a clearer understanding of what kinds of things can sensibly be characterized as rigorous. We began by talking about specific test questions, but Grant pointed out in the comments that rigor isn’t a characteristic of a question or a task: rigor is a characteristic of the resulting thinking and work.
How, then, does rigor factor into an evaluation of a test? I think one reasonable approach is to examine whether or not individual test questions are designed to produce a rigorous response.
As noted in Part 1, rigor is a subjective quality: it depends on a student’s knowledge and experiences. Since different students will have different experiences with a particular question, this poses an obvious challenge for test-makers if the goal is to design questions that produce rigorous responses. For example, the trapezoid problem discussed in Part 1 would produce a rigorous response for one kind of student but not for another.
Another significant challenge that arises in testing becomes apparent when we consider the lifespan of an exam.
In Part 1, we discussed the value of novelty in eliciting rigor from students. But while a novel kind of question might initially provoke a rigorous response, over time it may lose this property. As the question becomes more familiar, it will likely start admitting valid, but less rigorous, solutions. In short, it becomes vulnerable to gaming or test prep.
For example, consider this question about taxes and tips, from the recent NY state 7th-grade math exam.
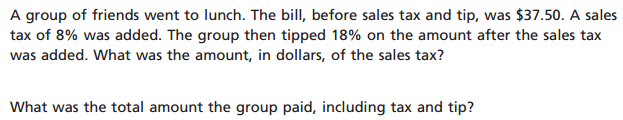
This problem is not particularly challenging, deep, or novel. According to the annotation, it “assesses using proportional relationships to solve multistep ratio and percent problems”. This may be true, but I see it as a pretty straightforward procedural problem. And while it technically it is a multi-step problem, the steps are pretty simple: multiply, multiply, add.
Let us, for the sake of argument, assume that this problem is likely to produce a rigorous response from students. The question now becomes, “How long can it reasonably be expected to do so?”.
There were a number of questions involving taxes and tips in the set of released 7th-grade math exam questions. This kind of question may have surprised test takers this time, but it’s easy to predict what will happen: students and teachers will become more familiar with this kind of problem and develop a particular strategy for handling it. Instead of seeking to understand the inherent proportional relationships, they will just learn to recognize “tax-and-tip” and execute the strategy.
This issue doesn’t just occur at the tax-and-tip level. Grant shared an old TIMSS problem in Part 1 about a string wrapped around a cylindrical rod, citing it as an example of a real problem, one that is very difficult to solve. It’s a great problem, and it would generate a rigorous response form most students; however, it didn’t generate a rigorous response from me. As someone who has previously encountered many similar problems, I was familiar with what Paul Zeitz would call the crux move: before I had even finished reading the question, I was thinking to myself cut and unfold the cylinder. Familiarity allowed me to sidestep the rigorous thinking.
That string-and-cylinder question put me in mind of a similar experience I had when I started working with school math teams. The first time I faced the problem “How many different ways can ten dollar bills be distributed among three people?” I produced a very rigorous response: I set up cases, made charts, found patterns, and got an answer. It took me several minutes, but it was a satisfying mathematical journey.
However, I noticed that many of the students had gotten the correct answer very quickly and with virtually no work at all. I asked one of them how he did it. “It’s a stars-and-bars problem,” he said. Confused, I questioned him further. He couldn’t really explain to me what “stars-and-bars” meant, but he did show me his calculation and the correct answer.
Later I learned that “stars-and-bars” was the colloquial name for an extremely elegant and sophisticated re-imagining of the problem. The dollar bills were “stars”, and the “bars” were two separators that divided the stars into three groups. The question “How many different ways can ten dollar bills be distributed to three people?” was thereby transformed into “How many different ways can ten stars and two bars be arranged in a row?”
A simple calculation provides the answer: 
Here, a challenging problem that generally demands an extremely rigorous response can be transformed into a quick-and-easy computation if you know the trick. The trick is elegant, beautiful, and profound; but is it rigorous? A reader suggested in a comment on Part 1 that only problems without teachable shortcuts should be used on tests, but is this possible? Few people know the above shortcut, but if this problem started appearing with regularity on important exams, word would get around. Once it did, test writers would have to go back to the drawing board.
In Part 1, Grant said that a condition necessary for rigor is that learners must face a novel, or novel-seeming question. Based on what I’ve written above, I think this makes a lot of sense. Novelty counterbalances preparation, so this is a great standard for rigor. But is this possible in testing? Like rigor itself, novelty is subjective: it depends on the experiences of the student. Since different students have different experiences, it seems like it would be extremely difficult to consistently produce novel questions on such a large scale.
And while a question might be novel at first, in time the novelty wears off. Students and teachers become more accustomed to the question and test-prepping sets in. The longer a test exists and the wider it reaches–that is, the more standardized it becomes–the harder it gets to present novel questions, to protect against shortcuts, and to provoke rigorous thinking.
Grant Wiggins Responds
Patrick, I think you have done a nice job of stating a problem in test-making: it is near impossible to develop test questions that demand 100% rigorous thought and precision in mass testing. There are always likely to be students who, either through luck or highly-advanced prior experience, know techniques that turn a demanding problem into a recall problem.
But what may not be obvious to educators is that the test-maker is both aware of this relative nature of rigor and your concern that certain problems can be made lower-order – yet, may not mind. In fact, I would venture to say that in your example of stars and bars, the test-maker would be perfectly happy to have those students provide their answer on that basis. Because what the test-maker is looking for is correlational validity, not perfect novel problems (which don’t exist). Only smart students who were well-educated for their grade level could have come up with the answer so easily – and that’s what they look for. The test-maker doesn’t look at the problem in a vacuum but at the results from using the problem in pilots.
By that I mean, the test-maker knows from the statistics of test item results that some items are difficult and some easy. They then expect and work to make the difficult ones be solved only by students who solve other difficult problems. They don’t know what your stars and bars kid were thinking; they don’t need to! They only need to show that otherwise only very able students also get that problem correct, i.e. whether by 6 step reasoning or fortunate recall and transfer, in either case this is likely to be a high-performing student.
Items are not “valid” or “invalid”. Inferences from results are either valid or invalid. At issue is not perfect problems but making sure that the able people score well and the less able don’t. That’s how validity works in test construction. Validity is about logic: what can I logically infer from the results on a specific test?
Why is logic needed? Because a test is a limited sample from a vast domain. I have to make sure that I sample the domain properly and that the results are coherent internally, i.e. that able kids do better on hard problems than less able kids and vice versa.
Simple example: suppose I give a 20-item arithmetic test and everyone gets 100 on it. Should we conclude that all students have mastered “addition and subtraction”? No. Not until we look closely at the questions. Was any “carrying” or “borrowing” required, for example? Were there only single-digit problems? If the answers were both no, then it would be an invalid inference to say that the kids had all mastered the two basic operations. So, I need to sample the domain of arithmetic better. I probably also need to include a few well-known problems that involve common misconceptions or bad habits, such as 56 – 29 or 87 + 19. Now, when I make this fix to my test and re-give it, I get a spread of scores. Which means that I am now probably closer to the validity of inferences about who can add and subtract and who can’t. (We’re not looking for a bell curve in a criterion-referenced test but the test-maker would think something was wrong if everyone got all the questions right. We expect and seek to amplify as much as we validly can the differences in ability, as unfair as that may sound.
This is in part why so many teachers find out the hard way that their local quizzes and tests weren’t hard enough and varied enough as a whole set. Their questions did not sample the domain of all types of problems.
So, the full validity pair of questions is:
- Can I conclude, with sufficient precision, that the results on a small set of items generalize to a vast domain of content related to these items? Are they, in other words, a truly representative sample of the Standards? Can I prove that this (small) set of items generalizes to results on a (large amount of content related to) Standards?
- The second question is: does this pattern of test results make sense? Are the hard questions actually hard for the right reasons (as opposed to hard because they are poorly worded, in error, a bad sample, or otherwise flawed technically) – so that only more able performers tend to get the hard ones right? In other words, does the test do a valid job of discriminating those who really get math from those who don’t? That’s why some questions properly get thrown out after the fact when it is clear from the results that something was wrong about the item, given the pattern of right and wrong answers overall and on that one item. This has happened a number of times in Regents and AP exams.
It is only when you understand this that you then realize that a question on a test may seem inappropriate – such as asking a 6th grader a 10th grade question – but “work” technically to discriminate ability. Like the old use of vocab and analogy questions.
Think about it in very extreme cases: if I ask an algebra question on a 5th grade test, the results may none the less yield valid conclusions about math ability – even though it seems absurd to the teacher. Because only a highly-able 5th grader can get it right, so it can help establish the overall validity of the results and more usefully discriminate the range of performance. Test-makers are always looking for usefully-discriminating items like that.
Here’s the upshot of my musings: many teachers simply are mistaken about what a test is and isn’t. A test is not intended to be an authentic assessment; it is a proxy for authentic assessment, constrained by money, time, personnel, politics, and the logistical and psychometric difficulties of mass authentic assessment. The state doesn’t have a mandate to do authentic assessment; it only has a mandate to audit local performance – and, so, that’s what it does. The test-maker need only show that the spread of results correlates with a set of criteria or other results.
A mass test is thus more like the doctor’s physical exam or the driving test at the DMV – a proxy for “healthful living” and “good driving ability.” As weird as it sounds, so-called face validity (surface plausibility) of the question is not a concern of the test-maker. In short, we can add a third topic to the list that includes sausage and legislation: you really don’t want to know how this really happens because it is an ugly business.
. This indicates that the test-makers either (a) don’t understand the concept of domain or (b) they have decided to start working in the world of complex-valued functions without telling the rest of us.
and 
, and note that 
. In order to evaluate 
, we first have to evaluate 
. But 
, which isn’t a real number. Thus 
.
. But we never talk about complex-valued functions in Algebra 2 / Trig. When we talk about functions like 
, we are always talking about real-valued functions. And just because the process of squaring later on down the line eliminates the imaginary part, that doesn’t fix the inherent domain problem. After all, what is the domain of 
?
