A Conversation About Rigor, with Grant Wiggins — Part 1
This is the first post in a dialogue between me and Grant Wiggins about rigor, testing, and the new Common Core standards. Each installment in this series will be cross-posted both here at MrHonner.com and at Grant’s website. We invite readers to join the conversation.
Patrick Honner Begins
After a spirited exchange on Twitter regarding New York State’s new Common Core-aligned tests, Grant Wiggins cordially invited me to continue our conversation about rigor in a collaborative blog post. It wasn’t until I saw his first suggested writing prompt—What is rigor?—that I suspected that perhaps I was being rope-a-doped by a master. But the opportunity was too intriguing to pass up.
While I don’t expect to flesh out a fully-formed, operational definition of rigor, our conversation brought a couple of important ideas to mind regarding what it means for a mathematical test question or task to be rigorous.
Higher grade-level questions are not necessarily more rigorous
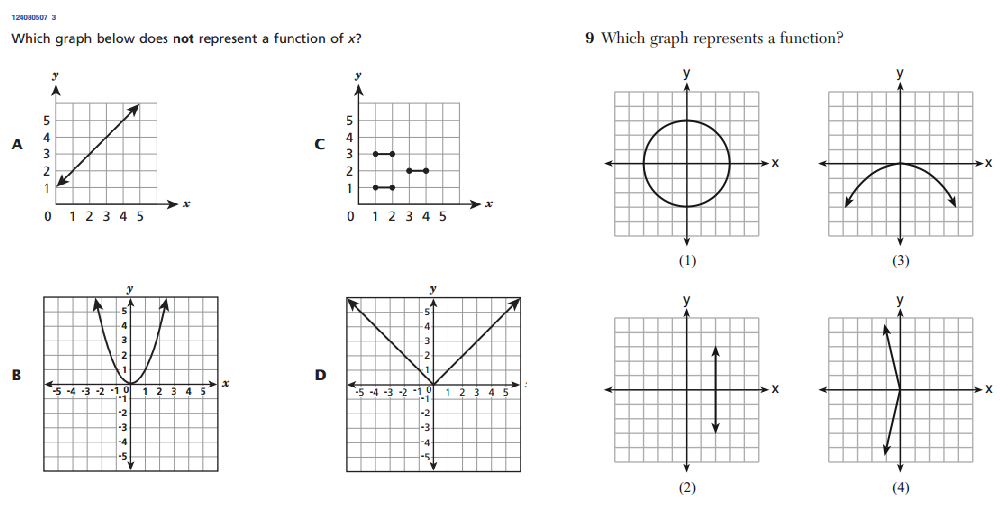
Our exchange began after I wrote a piece for Gotham Schools about the 8th grade Common Core-aligned test questions that were released by New York state. In reviewing the items, I noticed some striking similarities between these 8th grade “Common Core” questions and questions from recent high school math Regents exams.
Above on the left we see a problem from the set of released 8th grade questions, and on the right, we see a virtually identical question that appeared on this January’s Integrated Algebra exam, an exam taken by high school students at all grade levels. (This was one of many examples of this duplication).
The annotations that accompany the released 8th grade questions suggest that this question requires that a student understand that “a function is a rule that assigns to each input (x) exactly one output (y)”. In reality, this question simply tests whether or not the student knows to apply the vertical line test to determine whether or not a given graph represents a function. If the student recalls this piece of content, the question is simple; if not, there is little they can be expected to do. It’s hard to imagine this particular question meeting anyone’s standard for rigor: it is a simple content-recall question. It is not designed to elicit any deep thinking or creative problem solving.
I was highly critical of the exam-makers for simply putting high school-level problem on the 8th grade exam and calling it more rigorous. In our Twitter exchange, Grant pointed out that a 10th grade question could be considered more rigorous, however, if the 8th grader had to reason the solution out rather than simply recall a piece of content. This excellent point led me to think about the subjective nature of rigor.
Rigor depends on the solution, and thus, the student
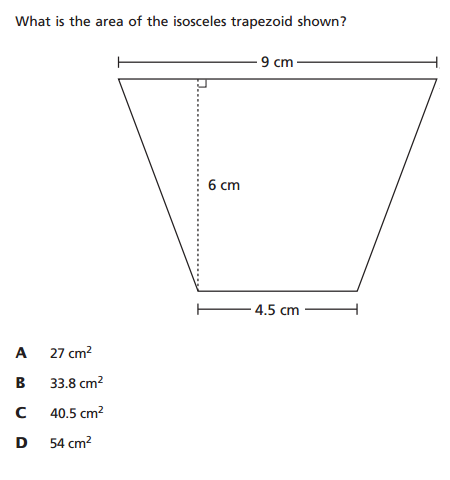
The following trapezoid problem from the 6th-grade exam is a good example of what Grant was talking about. It also illustrates the subjective nature of rigor.
Here, the student is asked to find the area of an isosceles trapezoid. According to the annotations, the student is expected to decompose the trapezoid into a rectangle and two triangles, use mathematical properties of these figures to determine their dimensions, find the areas, and then combine all of the information into a final answer. This definitely sounds like a rigorous task: the student is expected to think of a mathematical object in several ways, connect multiple ideas through several steps, and be precise in putting everything together.
The problem would be perceived much differently, however, if the student knew the standard formula for the area of a trapezoid (that is, area is equal to the product of the average of the bases and the height). Knowing that formula would make this a recall-and-apply-the-formula question, and not especially rigorous. Thus, this question might be considered rigorous in the context of 6th grade mathematics, but not in the context of 8th grade mathematics.
But if a 6th grade student happens to know the formula for the area of a trapezoid, they’ll get the answer faster while sidestepping all the messy details; that is, the rigor. And it won’t take long for students and teachers to realize that memorizing higher-level formulas might help them navigate these rigorous exams more efficiently and effectively. These rigorous questions, whose rigor depends in part on a lack of advanced content knowledge, might actually encourage some decidedly un-rigorous behavior in students and teachers.
Grant Wiggins Responds
I agree with your first two points. Just because a question comes from a higher grade level doesn’t make it rigorous. And rigor is surely not an absolute but relative criterion, referring to the intersection of the learner’s prior learning and the demands of the question. (This will make mass testing very difficult, of course).
To me, rigor has (at least) 3 other aspects when testing: learners must face a novel(-seeming) question, do something with an atypically high degree of precision and skill, and both invent and double-check the approach and result, be it in math or writing a paper. The novel (or novel-seeming) aspect to the challenge typically means that there is some new context, look and feel, changed constraint, or other superficial oddness than what happened in prior instruction and testing. (i.e. what Bloom said had to be true of any “application” task in the Taxonomy).
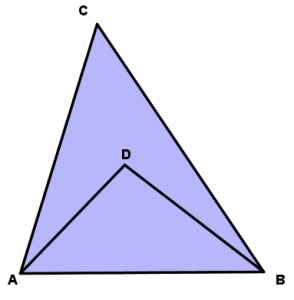
I would go further: depending upon context, a problem can go from hard to easy and easy to hard. Case in point – a great example from Michalewicz and Fogel’s book on heuristics:
“There is a triangle ABC, and D is an arbitrary interior point of this triangle. Prove that AD + DB < AC + CB. The problem is so easy it seems as if there is nothing to prove. It’s so obvious that the sum of the two segments inside the triangle must be shorter than the sum of its two sides. But this problem is now removed from the context of its chapter, and outside of this context the student has no idea of whether to apply the Pythagorean Theorem, build a quadratic equation, or do something else!
“The issue is more serious than it first appears. We have given this very problem to many people, including undergraduate and graduate students, and even full professors of mathematics, engineering and computer science. Fewer than 5% of them solved this problem within an hour, many of them required several hours, and we witnessed some failure as well.” (pp. 4-5)
It is helpful here to bring in Paul Zeitz and his clear account of the difference between an exercise and a (real) problem to flesh out my claim that rigor requires the latter, not the former (which is your point, too): “An exercise is a question that you know how to resolve immediately. Whether you get it right or not depends upon how expertly you apply specific techniques, but you don’t need to puzzle out what techniques to use. In contrast, a problem demands much thought and resourcefulness before the right approach is found.”
The first two authors go on to say that real problems are very difficult to solve, for several reasons:
- The number of possible solutions in the search space is so large as to forbid an exhaustive search for the best answer.
- The problem is so complicated…we need to use simplified models
- The evaluation function is ‘noisy’ or varies in time.
- The possible solutions are so heavily constrained that constructing even 1 feasible answer is difficult.
- The person solving the problem is inadequately prepared or imagines some psychological barrier that prevents them from discovering a solution.
To me the 2nd and 4th elements are key.
Here is one of my favorite such problems, from the TIMSS over a decade ago:
 Here’s what a NY Times Reporter wrote about this problem:
Here’s what a NY Times Reporter wrote about this problem:
“The problem is simply stated and simply illustrated. It also cannot be dismissed as being so theoretical or abstract as to be irrelevant for the technocrats of tomorrow. It might be asked about the lengths of tungsten coiled into filaments; it might come in handy in designing computer chips where distances are crucial. It seems to involve some intuition about the physical world and some challenge about how to determine something about that world.
It also turned out to be one of the hardest questions on the test. The international average of advanced mathematics students [in 12th grade] who got at least part of the question correct was only 12 percent (10 percent solved it completely). But the average for the United States was even worse: just 4 percent for a complete solution (there were no significant partial solutions).”
By EDWARD ROTHSTEIN (NYT); Business/Financial Desk, March 9, 1998, Monday
So, the challenge in math teaching – always! – is to come up with real problems, puzzling challenges that demand thought, not just recall of algorithms (mindful of the fact that in mass testing some kids will get lucky and have instant recall of such a problem and its solution).
My favorite sources? The Car Talk Puzzlers, and Math Competition books. But there is more to be said on the subject of ‘novel’ problems via mass testing.
Read Part 2 of the conversation here.
20 Comments
John Golden (@mathhombre) · August 14, 2013 at 11:10 am
It feels like rigor is getting tangled up with problem-solving here, as opposed to be a separate characteristic. As opposed to typical use, which almost always seems to be as a synonym of harder.
I’d prefer it to mean a certain level of mathematical precision. A proof is more rigorous than a solution which is more rigorous than an answer. Or in the Van Hiele sense of axiomatic thinking is more rigorous than formal argument which is more rigorous than informal argument.
MrHonner · August 14, 2013 at 1:36 pm
John-
As I started thinking about rigor as it applies to a math question or task, I definitely felt a bit tangled up with problem solving. I’m most comfortable with using the word rigor in describing a mathematical proof or argument, so I tried to think about how that would translate to a mathematical experience with some kind of question or task.
“Precision” was a key word Grant used as well in our initial back-and-forth. And I think precision is definitely an element of a mathematical proof. So, perhaps a rigorous question would demand precision from the solver?
Grant · August 14, 2013 at 2:32 pm
John: I agree that in this short post the two became conflated a tad, but I think our points still stands. Rigor is not merely about precision; it is not what we mean in education when we say: we want a more rigorous curriculum or test. I plan to clarify the definition of rigor further in the next post, but the gist of it is captured in the common distinction in athletics and performance arts assessment: both the degree of difficulty and the quality of performance have to be high. I agree with you point about arguments but that’s only half the battle: the argument has to be intellectually worthwhile, not just logically exact; it has to be about worthy tasks or problems.
l hodge · August 14, 2013 at 4:01 pm
I agree. Testing problem solving in a rigorous way, as in Grant’s terrific examples, seems to be testing intelligence as much as anything else.
So often we don’t really know how much a student understands and how much is more or less pattern recognition and memorized steps. A rigorous test should be able to sort out the difference. That doesn’t necessarily require “hard” questions.
For example, solve 3x + 1 = 7 has little rigor as a multiple choice question and not much more as a written answer. Instead ask which of the following are implied by the equation 3x + 1 = 7: 4x – 2 = x + 4, 3x – 6 = 0, 6x + 1 = 14? Or, the same thing except with 3x + 1 = k. To me these are rigorous even though they don’t require problem solving and are not that difficult for a student with a good understanding of solving linear equations.
MrHonner · August 14, 2013 at 7:12 pm
I like the idea that a “rigorous test” should be able to identify what a student really know, but it sounds like you’re talking about rigor a bit differently than I am: like a rigorous assessment-design by the teacher as opposed to a rigorous mathematical experience for the student.
And just to play devil’s advocate for a moment, are test questions that test “intelligence as much as anything else” (where the anything else is the intended curriculum) what we want on exams?
l hodge · August 14, 2013 at 7:56 pm
I probably wasn’t clear. My point is that too much of an emphasis on problem solving turns what is supposed to be a test of various standards into too much of an intelligence test – NOT A GOOD THING.
I think our definitions of rigor will overlap quite a bit. A rigorous test design (like I was talking about) will likely result in a rigorous mathematical experience for a large portion of the test takers. Of course just about any question could be a rigorous experience for at least a few students and completely routine for at least a few others.
For my classroom, I hope every student finds at least part of the test to be a rigorous experience. I don’t think that is important on a state test of standards, but is likely to be the case for the majority of students on a well written exam.
CCSSIMath · August 14, 2013 at 12:48 pm
We could try to summarize our notion here of the characteristics we like in a problem, but it would be impossible: that’s what our entire blog is about.
Nevertheless, the trapezoid problem is terrible on several levels, but not defective, which is one reason we didn’t review it.
In deciding where a given problem belongs, it is apparent that Common Core’s authors, curriculum writers and exam authors in general, and teachers don’t give enough consideration to our most important criterion: is a task grade-appropriate? This issue is relevant not only in mathematics, but in all grade school subjects. We’ve witnessed far too many examples of students involved (“engaged”) in tasks that are generally beneath their capacity; indeed, whenever students are having “fun”, it’s likely what they are doing is not intellectually challenging, and in our opinion, educationally useless.
Of course, when a teacher requires students to work hard, students complain and parents complain; then the administration berates the teacher for not being “invisible” in the classroom. Nothing makes an administrator happier than to see teachers in their classrooms…seen through the window and not heard about.
As for the trapezoid problem, it contains both a useless distraction and a needless dumbing down aspect. The dumb down feature is that it need not be “isosceles”; that doesn’t change the answer, but simplifies the problem into nothing more than a series of calculations. The unnecessary distraction is using a decimal value, which will catch students who are weak in decimal calculations, but otherwise understand the notion of the task. Two disjointed mathematical skills shouldn’t be tossed together in the name of “rigor” just because they can; there should be a better connection.
Finally, we won’t rehash our blog post that argues such a problem (sans decimals) really belongs in Grade 3, not Grade 6, because there’s nothing overly challenging there.
But the problem can easily be improved. If the trapezoid is drawn as obviously not “isosceles”, then when students decompose it into triangles, the problem becomes genuinely interesting because each triangle’s base cannot be individually determined, but the problem is still solvable. That’s a great abstraction for elementary school students.
That higher-level feature is in this problem as well:
http://fivetriangles.blogspot.com/2012/04/17-area.html
We agree that knowing the trapezoid area formula sidesteps any challenge, which is why we prefer problems in which there are no teachable shortcuts, rendering moot questions of whether a problem’s characteristics change pre- or post-formula.
As an example, this question has a trapezoid, but isn’t significantly shortened by memorizing formulas:
http://fivetriangles.blogspot.com/2013/04/65-paper-cuts.html
It was given to year 6 students: we think it is grade-appropriate because there’s no more advanced skill needed than what year 6 students are expected to know, yet it combines several mathematical skills usefully.
MrHonner · August 14, 2013 at 2:07 pm
A provocative statement like “If kids are having fun they aren’t being intellectually challenged” may be fun to make, but it’s not relevant to this discussion and only serves to distract, and possibly dissuade, conversation. I would like the conversation to stay focused on rigor, mathematics, and testing.
Your characterization of making the trapezoid isosceles as a “dumbing down” of the problem is interesting. Solving the problem for a non-isosceles trapezoid would certainly be more challenging (again, assuming no knowledge of the formula), although I don’t see the isosceles trapezoid problem as inherently dumbed-down; it’s just simpler (in a substantial way).
I like the point that tossing together disjointed skills (here, the geometry and the handling of decimals) does not necessarily produce rigor, although I suppose being able to manage the disjointed aspects of a problem is an important mathematical skill.
When it comes to grade-level, I admittedly don’t think much about what’s appropriate for elementary school students. In general, appropriateness to me is primarily a function of the individual. I don’t know how sweeping pronouncements about when students should be learning what get made.
Glenn · August 14, 2013 at 6:53 pm
I, too, question the difference between problem solving and rigor.
For instance, on the trapezoid problem we could ask one level of learner to find the area of the trapezoid as given, a higher level of learner would be given algebraic expressions for the values, while the geometry learner would be asked to derive the area via the deconstruction.
These three different problems all start from the same point, a trapezoid, but have different levels of rigor and cognitive demands. I know it isn’t always true that just replacing a value with an algebraic expression creates more rigor, but that is one possible way to introduce more rigor. Replacing an integer with a fraction also can increase rigor depending on the objectives of the course.
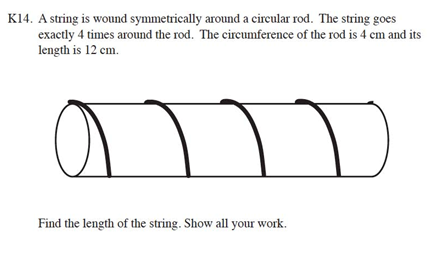
The last problem is rigorous, but not because of the material or concepts, but because the learner needs to realize the tube can be cut and flattened creating a Pythagorean theorem triple 3-4-5 right triangle. That is not more rigorous “mathematics” but more rigorous problem solving (which is mathematics, but a different kind of rigor in mathematics.)
Grant · August 15, 2013 at 8:11 am
A problem isn’t rigorous; a student’s thinking and work need to be rigorous. It requires rigorous thinking and persistence to solve the tube problem.
Glenn · August 15, 2013 at 10:11 am
Grant, I am not sure the tube problem really does require rigorous thinking and persistence to solve the problem. As I see the the problem, it requires creativity.
The creative part is realizing that you can cut the tube down the side and lay it out flat. Once that is done you have 4 3-4-5 triangles. The mathematics of the problem is really around 5th grade (or lower), but the problem solving / creativity required in the problem is high school level. If I claim that the mathematics of the problem is rigorous I am making a false claim.
The problem is we typically don’t teach learners to be creative in math class; we teach them to be very algorithmic and step by step.
I guess the real problem is am I making a false distinction between “mathematics” and “problem solving” in this discussion. To me it seems there is a distinction to be made, but is that a real distinction or a false one?
Grant · August 15, 2013 at 10:21 am
Again, the fact that the problem requires creativity or not is not what makes a demand rigorous. Rigor is not a trait of a problem but a demand on the learner. Recall the component parts of my definition: demands hard thinking, demands great precision, involves novel context or set-up. The tube problem arguably fits, therefore. The fact that you had no difficulty finding the solution path is no different than saying my daily walking regimen is not at all rigorous for you. If only a tiny fraction of 18 year olds came up with a sound solution, I would say that this problem was ‘rigorous’ for them, so for almost all 18 year olds tested it met the requirements of the learner being challenged in at least 2 of the 3 ways (I grant you that painstaking precision was not required here).
Put differently, what’s your response to the triangle problem from M & F in my post? I took their challenge and it took me over an hour to solve it – and my knowledge of Euclidean geometry is very strong. Out of context, a problem is much harder – and in many tests that is what makes the results typically worse than local testing. As soon as you know that this is not a HS problem but a problem for younger grades it no longer requires rigor; it becomes ‘easy’.
Glenn · August 15, 2013 at 10:28 am
I understand much more clearly now the focus and point of the definition of “rigor”. Thank you!
I think I am still stuck between the demands placed on us by the state & district assessment requirements and the much much more careful thinking about rigor that you have challenged us with.
I can see some very rich conversations with my district leaders on this topic and using this definition for use in class.
I look forward to the rest of the posts in this thread.
Grant · August 15, 2013 at 8:15 am
Think of a workout. A workout is rigorous if it requires you to raise and keep raised your heart-rate and generate lactic acid. But only at the upper-most reaches of modern athletics is this an absolute requirement; as we say in the Post, for most of us it is relative. What you would find as a comfy training run would be a rigorous workout for me. So, you can’t just look at the problem. You have to look at the learner working the problem.
MrHonner · August 15, 2013 at 9:19 am
As I’ve been writing and thinking about this, I have at times been confused as to what exactly I was describing as rigorous: a solution, a problem, a test (a l hodge mentions above). This conversation, including the comments, has helped me become aware of the many different ways the word rigor is used.
I suppose in thinking of a particular problem or task as rigorous, what I’m thinking is that the problem is designed to produce a rigorous response. Which sounds good to me, until I start thinking about the subjective nature of student responses.
Glenn · August 15, 2013 at 10:22 am
This response clarifies the question I just posed, is it a false distinction I was making?
I think you are saying yes, because I am only focusing on the problem, and not also thinking about the learner who is doing the problem. The tube problem is not rigorous to me because I can think creatively about and with math.
But now I am stuck. Our current assessment models require “rigor” to be assessed uniformly, not individually. But if rigor is something that must be considered at the level of the individual learner, we will not really be able to assess it the way we are told to assess.
And if rigor is in large part about creativity in problem solving, then we, as math teachers, are in double trouble because creativity is very difficult to teach.
Sue VanHattum · August 15, 2013 at 11:04 am
l hodge gave a great example of a problem s/he considers rigorous but not problem-solving. Do you agree, Grant and MrHonner? I’d like to tease out how rigorous questions are different from questions that require problem-solving. And I’d like to think about more examples.
I think we can always get a little more creative in the way we ask questions, so that they are not routine for any of the students, but also do not ask for leaps of creativity.
For example, to test whether students understand the concept of slope, rather than the technical implementation, we can simply show a line (no coordinates) and ask for an estimate of the slope. What is the slope of / ? a. 2 b. 1/2 c. -2 d. -1/2
Grant · August 15, 2013 at 11:16 am
While I like the query as a test of understanding of the concept of slope, given my definition it doesn’t pass. For one thing, LESS precision than normal is required. For another, if you were taught the concept of slope, you would not find this much an intellectual stretch. Rather, what it does well (to use test construction language) is it acts as a really good discriminator of who gets it and who doesn’t – i.e. valid but not taxing and rigorous. I plan to return to the question of valid discriminators in a future post because it is something most educators do not realize: test-makers look for valid discriminators and often some of the best ones lack face validity to teachers. Hint: the infamous pineapple question in NY on the ELA last year was a valid discriminator for what was being tested.
Here is another example, from Van de Walle that I often use in workshops with teachers. “Given the relationship of feet to yards, frame the mathematical relationship in an equation using Y for yards and F for feet.” MOST people, including advanced students, write 3F = Y (which is wrong, of course, but revealing of one’s understanding of the math vs English language, or lack of it).
Mike Lawler · August 15, 2013 at 12:00 pm
While I enjoyed reading this piece and look forward to the next one(s), I find myself pretty much in full agreement with the points made by both Mr. Honner and Mr. Wiggins. As a result, I feel as though I’m not fully appreciating the purpose of the conversation.
Is there a central point of disagreement between the two authors, or is the goal to flush out are more precise definition of “rigor” in the context of exam questions? (or something else entirely?)
Thanks
Grant · August 15, 2013 at 9:54 pm
I would say that our goal is the latter, but broader – flush out some ideas that are either implicit in lots of conversations about standards and testing – rigor, in this case – or otherwise needing greater clarity or precision because they are being carelessly thrown about.