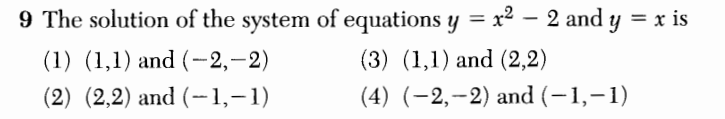Testing

Teaching Testing

Regents Recap — June 2014: Which Graph is Steeper?

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The following question appeared on the June, 2014 Algebra 2 / Trig exam. To start, steeper is not a well-defined term, not in an Algebra 2 / Trig class, anyway. I’m not against using the word in everyday mathematics conversations, but I’m not a fan of putting it on an official exam like this. After all, I think these exams should model exemplary mathematical behavior. But that’s not the real issue here.

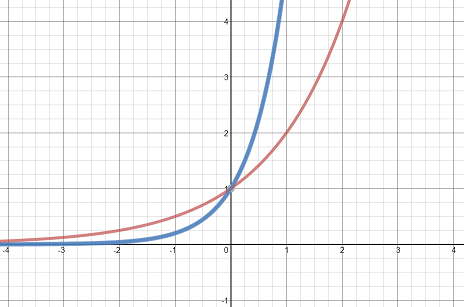
Even if we accept what steeper means, it can not be said that either graph is steeper than the other. Take a look: here, $y = 2^{x}$ is graphed in red and $y = 5^{x}$ is graphed in blue.

It seems pretty clear that the blue graph is steeper than the red on the right hand side, it also seems pretty clear that the red graph is steeper off to the left.

To be precise, the derivative of $y = 2^{x}$ is greater than the derivative of $y = 5^{x}$ for $x < \frac{ln(\frac{ln5}{ln2}}{ln(2) - ln(5)} \approx -0.9194$ , thus making the red graph steeper for those values of x.

Thus, there really is no correct answer to this question. The answer key originally had (3) as the correct answer, but it is no truer than (2). Ultimately, a correction was issued for the problem, and both (2) and (3) were awarded full credit.

Mistakes are bound to happen when writing exams, and it’s good that a correction was ultimately issued. But this is a pretty obvious error. This question should not have made its way onto a high-stakes exam taken by tens of thousands of students. A thoughtful student might have been frustrated, confused, or disheartened confronting this question with no correct answer. Hopefully its impact didn’t extend beyond these two points.

By MrHonner, 10 years10 years ago

Teaching Testing

Regents Recap — June 2014: What is an “Absolute Value Equation”?

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The following question appeared on the 2014 Integrated Algebra exam.

My question is this: what, exactly, is an “absolute value equation”? According to the scoring key, the correct answer to this question is (2). This suggests that the exam writers believe an “absolute value equation” to be some transformation of $y = |x|$ .

But “absolute value equation” is not a precise description of what the exam writers seem to be looking for. It would be hard to argue that $y = |2b^{x}|$ is not an “absolute value equation”, but that appears to be the graph depicted in (1). With some work, all the given graphs could be represented as equations involving absolute values (an exercise left to the reader).

I doubt this imprecision caused any student to get this question wrong, but as I have argued again and again, these exams should stand as exemplars of mathematical precision. These exams should not model imprecise language, poor notation, and improper terminology. We do our students a great disservice by constantly asking them to guess what the exam writers were trying to say.

By MrHonner, 10 years10 years ago

Geometry Teaching Testing Uncategorized

Regents Recap — June 2014: When Good Math Becomes Bad Tests

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

It is a true geometric wonder that a triangle’s medians always intersect at a single point. It is a remarkable and beautiful result, and the fact that the point of intersection is the centroid of the triangle makes it even more compelling.

This result should absolutely be a part of the standard Geometry curriculum. It important and beautiful mathematics, it extends a fundamental notion of mathematics (symmetry) in new ways, and it is readily accessible through folding, balancing, compass construction, and coordinate geometry.

But here’s what happens when high-stakes testing meets meaningful mathematics.

This wonderful result has been reduced to an easy-to-test trick: the centroid divides a median in a 2:1 ratio.

It’s not hard to see how such a fact can quickly become an instructional focus when it comes to centroids: if that’s how it’s going to be tested, that’s how it’s going to be taught. Of course, teachers should do more than just teach to a test, but there’s a lot riding on test results these days, and it’s hard to blame teachers for focusing on test scores when politicians, policy makers, and administrators tell them their jobs depend on it.

This is just one example of many, from one test and one state. This is an inseparable component of standardized testing, and it can be found in all content areas and at all levels. And for those who argue that the solution is simply to make better tests, keep this in mind: New York has been math Regents exams for over eighty years. Why haven’t we produced those better tests yet?

By MrHonner, 10 years10 years ago

Teaching Testing

This is Not an Exponential Function

A question from the January 2014 Integrated Algebra Regents exam asks students to identify a graph showing exponential decay. This graph was the correct choice.

We regularly see terrible graphs on these exams: non-trigonmetric trig functions, functions intersecting their vertical asymptotes, and unscaled coordinate systems. So it comes as no surprise that this graph is not actually the graph of an exponential function!

First, note that all exponential functions have the form $y = C a ^{kx}$ . Since this graph passes through the point (0,4), we immediately see that $C = 4$ .

Note also that the graph passes through the point (2,1). Thus, $y(2) = 4 a ^{2k} = 1$ . We can now use this information to compute $y(1)$ .

Since $4 a ^{2k} = 1$ , we see $a^{2k} = \frac{1}{4}$ . But $a^{2k} = (a^{k})^{2}$ , and so $(a^{k} )^{2} = \frac{1}{4}$ .

Taking the square root of both sides, we see that $a^{k} = \pm \frac{1}{2}$ . Assuming $a > 0$ , we have $a^{k} = \frac{1}{2}$ , and so $4a^{k} = 2$ . But $y(1) = 4 a ^{k}$ , so we now know that $y(1) = 2$ .

Notice, however, that the graph does not pass through the point (1,2)! Thus, this is not the graph of an exponential function.

Related Posts

By MrHonner, 11 years8 years ago

Teaching Testing

Regents Recap — January 2014: Systems of Equations

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Solving systems of equations is a fundamental mathematical skill. Systems come up in a variety of mathematical contexts, and so they play a natural role in all high school math courses.

It’s not surprising, then, that solving systems of equations appear on all New York math Regents exams. But what is surprising is how similar the questions on different exams are, given that the three exams span 3-4 years of mathematical learning.

For example, here is a problem from the Integrated Algebra exam.

Here is a problem from the Geometry exam.

And here is a problem from the Algebra 2 / Trig exam.

The question from the Integrated Algebra exam is actually harder than the question on the Geometry exam. Ironically, the directive on the algebra exam is to solve the equation graphically.

The system on the Algebra 2 / Trig exam involves rational expressions and a quadratic equation, but these are skills students are supposed to have in the Integrated Algebra course, which they take 2-3 years earlier.

I have written about this phenomenon before, but it continues to strike me as odd that over the span of 3-4 years of mathematics instruction, this is the growth these tests are looking for.

By MrHonner, 11 years11 years ago

Follow Mr Honner