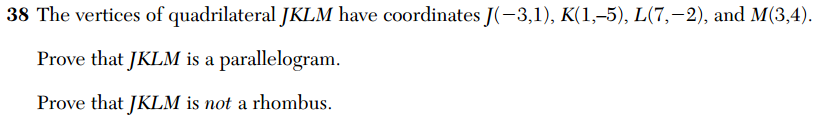Testing

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The following item appeared on the 2014 Geometry exam.  It was the highest-valued item on the exam, the only six-point question.

There’s nothing particularly unusual about this problem.  In fact, similar problems have appeared on prior exams.  Here we see the lone six-point problems from the 2013, 2011, and 2010 Geometry exams.

The problems are all very similar, yet there is one subtle difference between the 2014 version and these three prior versions:  the 2014 version contains one less substantial task than the three previous versions.  That is, it requires less work than previous versions, but is still worth six points.

In 2014, the student is asked to prove that a given quadrilateral is a parallelogram, but not a rhombus.  In 2010, the student had to do these two things, but in addition prove that the quadrilateral wasn’t a rectangle.

In 2013 and 2011, the student was asked to prove two similar results, but first had to construct a new quadrilateral from the given quadrilateral.  This preliminary work involves repeated application of the midpoint formula.

I don’t really think this is a big deal, but it does point to the subtle ways in which tests, scores, and results can be manipulated.  Test results have become highly politicized in recent times:  politicians routinely take credit for improving graduation rates and closing achievement gaps.  But without scrutiny of the tests themselves–their content, their construction, their scoring–it’s difficult to put such claims in their proper perspective.

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The following question appeared on the June, 2014 Algebra 2 / Trig exam.

Graphs without scales are common on Regents exams (I’ve written about this before).  Personally, it’s not a huge deal to me–I’m a lazy grapher, myself.  However, a colleague of mine regularly complains about this, and she made an excellent point regarding the grading of this particular problem.

The solution to this problem involves translating the graph one-unit to the left and two units up.  But since no scale is given on the graph, it’s not clear what one unit to the left would be.  If we assume the box on the graph indicates one unit, then the red graph below would be appropriate.  But if we assume a box to represent half-a-unit, the purple graph would be correct.

If no scale is explicitly given, it seems like both graphs should be considered correct and receive full credit.  But the rubric doesn’t address this possibility, and it’s unlikely students were given the benefit of the doubt.

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Elementary statistics plays an increasing role in high school math curricula, but the ways these concepts are often tested raises some concerns.  After all, the manner in which ideas are tested can reflect how the ideas are being taught.

Here’s a question from the 2014 Integrated Algebra exam:  which of the following is not a causal relationship?

Causality is notoriously difficult to establish, but I’ll set aside my philosophical objections for the time being.  My primary concern here is with (2) being the correct answer.

First, correlation is a relationship between two quantities.  What quantity is population correlated with in answer choice (2)?  “The taking of the census” is an event, not a quantity.  This may seem like nitpicking, but what quantity are we supposed to assume in its place?  It seems natural to assume “the census taken” to mean “the number of people recorded on the census”, but then how could there be no causal relationship?  What causes a number to be written down for “population”, if not the actual population?

Here’s another question from the 2014 Integrated Algebra exam.

It’s important to talk about bias in surveys, but no substantial thought is required to answer this question:  three of the answer choices have absolutely nothing to do with campsites.  And for the record, the question should really be phrased like “which group is most likely to be biased against the increase?”.

And this is a problem typical of the Algebra 2 / Trig exam.

I know it’s pretty much standard usage, but no finite data set can be normally distributed.  The correct terminology here would be something like “the heights can be approximated by the normal distribution”.

I’m aware that some may see these complaints as minor, but as I’ve argued before, I think it is extremely important to model precision and rigor in mathematical language for students.  We expect this from our teachers and our textbooks; we should expect it, too, from our tests.