Regents Recap — January 2013: Where Does This Topic Belong?
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
There seems to be some confusion among the Regents exam writers about when students are supposed to learn about lines and parabolas. Consider number 39 from the January 2013 Integrated Algebra exam:
Compare the above problem with number 39 from the June 2012 Geometry exam:
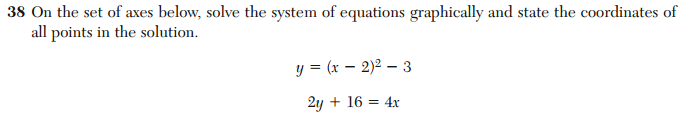 These questions are essentially equivalent. They both require solving a system of equations involving a linear function and a quadratic function by graphing. Yet, they appear in the terminal exams of two different courses, that are supposed to assess two different years of learning.
These questions are essentially equivalent. They both require solving a system of equations involving a linear function and a quadratic function by graphing. Yet, they appear in the terminal exams of two different courses, that are supposed to assess two different years of learning.
When, exactly, is the student expected to learn how to do this? If the answer is “In the Geometry course”, the Algebra teacher can hardly be held accountable if the student doesn’t know how to solve this problem. And if the answer is “In the Integrated Algebra course”, what does it mean if the student gets the problem wrong on the Geometry exam? Is that the fault of the Geometry teacher or the Algebra teacher? The duplication of this topic raises questions about the validity of using these tests to evaluate teachers.
And if that isn’t confusing enough, check out this problem from the 2011 Algebra 2 / Trig exam.
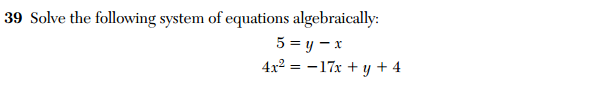 Here, we see the same essential question, except now the student is required to solve this system algebraically. These three exams–Integrated Algebra, Geometry, Algebra 2/Trig–span at least three years of high school mathematics. In the integrated Algebra course, a student is expected to solve this problem by graphing. Then, 2 to 3 years later, a student is expected to be able to solve the same kind of problem algebraically.
Here, we see the same essential question, except now the student is required to solve this system algebraically. These three exams–Integrated Algebra, Geometry, Algebra 2/Trig–span at least three years of high school mathematics. In the integrated Algebra course, a student is expected to solve this problem by graphing. Then, 2 to 3 years later, a student is expected to be able to solve the same kind of problem algebraically.
What does that say about these tests as measures of student growth?

6 Comments
Five Triangles · February 28, 2013 at 5:10 pm
We agree teachers are being caught in a bind, but our biggest objection to such Regents questions is whether in any grade, be it 9th, 10th or 11th, the questions can ever say much about student achievement.
They are the type of problem that is still almost universally taught by demonstrating in class and having students practice the procedure with, as you wrote, “essentially equivalent” examples.
We don’t think that demonstrating competence at practiced procedures on an exam will ever be a reliable measure of “student growth”.
We like problems like this:
http://fivetriangles.blogspot.com/2012/04/quadratic-functions.html
that require the same skill set with straight lines and parabolas, but take the concepts further.
And yes, it should be crystal clear in which year such topics are explored and assessed.
MrHonner · February 28, 2013 at 6:37 pm
Your objection to these kinds of questions is of course valid, as these exams are almost entirely composed of textbook problems. It’s safe to say that there isn’t a compelling mathematics problem on any of these exams.
The problem you linked to is nice, and certainly requires a deeper level of understanding in order to work through. While having higher quality questions on important exams would be a positive thing, it only address part of one of the many serious problems with this system.
And the validity that comes from the novelty of these deeper questions will only last as long as the commitment to consistently produce them. In the long run, even high quality tests get gamed eventually (see: AP Calc).
Joshua Bowman (@Thalesdisciple) · February 28, 2013 at 9:29 pm
This is an interesting observation in light of this evening’s #mathchat discussion (into which I merely dipped my toe): part of the discussion centered around the idea that insisting math topics must be covered in a certain linear order is a misconception. In particular, this would seem to belie Five Triangles’ comment that “it should be crystal clear in which year such topics are explored and assessed.” This post seems to be a case of conflict between established statewide curricula and standardized testing—both of which are problematic.
Basically, while I agree that it’s troublesome to see these nearly identical problems appearing on end-of-year tests at three different levels of schooling, I wonder if you’re using this as an example of “The testing board can’t be bothered to check what the curricula say, which is why standardized tests have problems”, or as a symptom of a greater “Standardized tests are inherently detrimental to education.”
MrHonner · February 28, 2013 at 9:39 pm
Can it be an example of both?
I agree that the idea of a correct “sequence” of mathematical instruction is somewhat artificial, but if you’re going to operate a large-scale, top-down education system, you have to provide some kind of guidelines (curricula; standards; tests; etc). And if those guidelines aren’t consistent, what good are they?
As to the second point, the more I think about it, the more I believe that standardized tests really are detrimental to education.
Joshua Bowman (@Thalesdisciple) · February 28, 2013 at 9:48 pm
It can absolutely be an example of both! I just wanted to know if that’s what you meant. 🙂
I need to consider what it means that I believe in large-scale support for education, but not large-scale management of education. Not tonight, though; still more grading to do…
Jerome Dancis · March 4, 2014 at 11:27 am
A problem that requires solving a system of equations, which is one step up from these Regents items is:
Praxis II Sample (constructed response) Question on Algebra. (Abbreviated) Graph (by hand) the circle, x^2 + y^2 = 25. Find the points on the circle you graphed, whose y-coordinate is twice its x-coordinate. Then find the [actual] coordinates of the points.
This was the only real Algebra question on the Praxis II so-called “Middle School math” content exam (#0069) from a decade ago. Middle school Math teachers got to use calculators on this exam (It was on the web at ftp://ftp.ets.org/pub/tandl/0069.pdf).
A sample response, which Praxis graded as “Demonstrates a sufficient knowledge of subject matter, concepts, theories, facts, procedures, or methodologies relevant to the question” had
four points listed: (2,4), (2,-4), (-2,-4), (-2,4). The theoretical “applicant” then used algebra, almost correctly calculated exact answers, but once again obtained four answers, two correct and two blatantly wrong. The answer suggests that the “applicant” is not aware that points, whose y-coordinate is twice its x-coordinate, must lie on the line y = 2x.