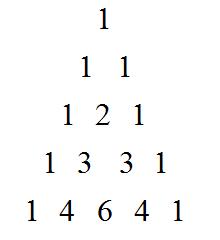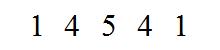Pascal’s Triangle is one of the most well-known mathematical constructions in human history. Named after Blaise Pascal, the triangle is rich in patterns and famous number sequences. The first five rows are shown below.
There are many ways to produce Pascal’s Triangle, but the typical way is to define every number as the sum of the two numbers above it: the one above on the right and the one above on the left. If there isn’t a number, then just use zero. For example, 4 = 1 + 3, and 6 = 3 + 3.
The ubiquity of Pascal’s Triangle makes it even more remarkable that a group of three junior high school students have recently collaborated on a paper published in the College Mathematics Journal that uses the famous triangle to find a new number pattern!
Apparently the story begins with one of the students confounding their teacher by insisting that the fifth row of the triangle should be
Despite the teacher’s attempts to “correct” them, the students produced a valid recursive relationship for the new triangle, which they describe as ( East * West + 1 ) / North. They then went on to link their definition to a known sequence in the Online Encyclopedia of Integer Sequences and Voila!, mathematical immortality!
As if the story of three eighth-graders publishing a paper in a college mathematics journal isn’t cool enough, the students collaborated entirely via the internet: one lives in Washington State, one in Alberta, Canada, and one in Indonesia!
A truly inspiring and remarkable story, and an object lesson in encouraging students to pursue their “wrong” answers!
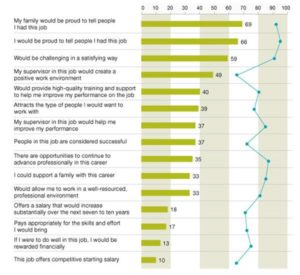This is a very interesting report from the business consulting firm McKinsey about why top students in U.S. colleges don’t want to become teachers.
