Here are the most popular posts from MrHonner.com for 2013.
 |
 |
 |
| Two-Dimensional Geometric Series | Happy Right Triangle Day! | Four Big Ideas in Algebra |
 |
 |
 |
| More Trouble With Functions | Decomposing Functions Into Even and Odd Parts | How Old is the Oldest Person You Know? |
My latest piece for the New York Times Learning Network is a lesson about currency based on Bitcoin, the digital commodity that has captured the interest of speculators, bankers, and regulators worldwide.
The rise of Bitcoin creates an interesting opportunity to explore the fundamental properties of currency. Where does currency get its value? Why and when are currencies accepted in exchange for goods and services? Who guarantees the security and stability of a currency?
On top of the basic questions of currency, the mining of Bitcoins (the curious and complicated process for creating new money) is rooted in mathematics and raises its own interesting questions
Most currencies have the property that new money can simply be printed, but where do the new bitcoins come from? They are “mined,” which has become a competitive business opportunity for participants. Paul Krugman describes this process of mining as “a drastic retrogression” that is as fundamentally foolish as relying on gold and silver was a century ago.
You can find the entire lesson here.
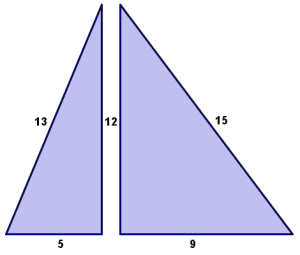
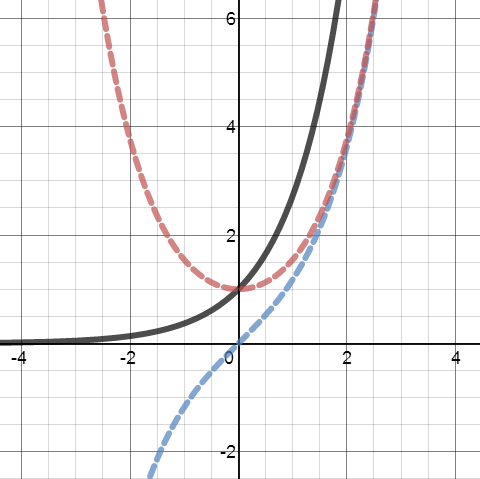
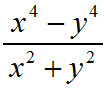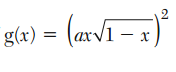This October I had the great pleasure of meeting Fields medalist Cedric Villani. Professor Villani gave an illuminating and accessible talk about his innovative work in the study of curvature, and afterwards spent some time hanging out and chatting with a few of the attendees.
Villani is a charismatic and engaging speaker, and he provided a lot of to think about in his talk. One remark that particularly struck me was
“Mathematics, in some sense, will always involve a little pain.”
The idea resonated with me but I was curious what he meant, so I asked him about it. I was a bit surprised when he said that mathematics is unnatural, and unnatural things are always painful.
I pressed him a bit, as I didn’t quite understand. “What are the first things you learn in physics?” he asked. He was alluding to Newton’s Laws, and in particular the law of inertia: An object at rest tends to stay at rest, and an object in motion tends to stay in motion. Villani grabbed a fork from across the table, slammed it down in front of him, and gave it a push. The fork slid a short distance and stopped. “This is absurd!” he said. “It does not stay in motion!”
Physics, that is, the laws of physics, are abstractions of our experiences with the real world. Understanding that when you push something, it will stop, is natural for us; understanding the law of inertia is not. This law is an abstraction of our natural experiences, and as such, is unnatural. He went on to argue that mathematics, too, is a collection of abstractions from our experiences of the real world, and therefore is unnatural.
He made an analogy with speaking and reading: speaking is natural for humans, we are hard-wired for it. But writing is not. It does not come naturally to us. As an abstraction of speaking, writing will always be difficult for humans to learn. It will always involve a little pain. Like mathematics.
Some world-class mathematics, a little philosophy, and a mathematical autograph! All in all, a pretty good evening.
I was proud to be a part of Math for America’s second annual MT^2 event , Master Teachers on Teaching.
MT^2 invites MfA teachers from around New York City to propose short talks related to the conference theme. This year’s theme was Change, and the seven teachers selected to present offered many different and interesting interpretations of that theme, including changing our practice, changing how we see our students, and changing the rules in mathematics.
At this year’s event, I offered a lighthearted but sincere take on my mathematical relationship with change. At last year’s inaugural event, where the theme was Modeling, I talked about how standardized testing often works against our attempts to teach proper mathematics (the video of the talk can be seen here).
This event is typical of how Math for America celebrates and empowers teachers. They created a space where teachers could share their ideas, grow their practice, and interact around mathematics, science, and teaching, and it was all teacher-led and teacher-driven. Several hundred teachers were inspired by the work of their peers, challenged to think differently, and encouraged to continue to strive to be better teachers. It’s great professional development, and it was a fun evening!
I am huge fan of Desmos, the free online graphing calculator. I use it almost every day in my classroom: to sketch simple graphs, demonstrate mathematical relationships, and dynamically explore mathematical situations. And like most worthy instructional technologies, it’s really a learning technology: it’s easily accessible to students as well as teachers..
As far as technology goes, Desmos works very well. But some of my favorite mathematical questions arise when technology does something we don’t expect.
For example, here’s the graph of 
But look what happens when you zoom in around the hole:
At a very small scale, some very curious behavior emerges!
Now, it’s not the function here that’s behaving strangely: its behavior is well-understood. It’s the mathematical technology that is behaving strangely, as it tries to represent the function.
Lots of interesting questions emerge from such anomalies, and these are great questions for students to explore. In doing so, they’ll not only learn some mathematics and some computer science, but they’ll also develop a healthier relationship with technology, by learning to understand how it does what it does, and perhaps more importantly, what it doesn’t do. I explore this theme in greater depth in my talk “When Technology Fails“.
You can find more of my work with Desmos here.
Related Posts
