Decomposing Functions into Even and Odd Parts

Published by MrHonner on May 21, 2013May 21, 2013

When it comes to functions, the concepts even and odd have always been important to me as a teacher. Connecting the algebraic and geometric representations of mathematical ideas is a primary goal in my classroom, and these concepts provide great opportunities to do that.

Algebraically, a function is even if $f(-x) = f(x)$ , and this condition manifests itself geometrically as symmetry with respect to the y-axis in the graph of $y = f(x)$ . A function is odd if $f(-x) = -f(x)$ , and geometrically this means that the graph of $y = f(x)$ is symmteric with respect to the origin. Knowing a function is even or odd provides a wealth of information to work with, and can make solving some problems trivially easy.

But it wasn’t until recently that I learned the following amazing fact: Functions can essentially be uniquely decomposed into even and odd parts!

Claim: Let $f(x)$ be a non-zero, real-valued function whose domain is symmetric about the origin; that is, $f(x)$ exists implies $f(-x)$ exists. Then $f(x)$ can be uniquely expressed as the sum of an even function and an odd function.

Proof: For any function $f(x) \neq 0$ , define the functions $a(x)$ and $b(x)$ in the following way:

$a(x) = \frac{f(x)+f(-x)}{2}$ and $b(x) = \frac{f(x)-f(-x)}{2}$

First, we see that

$a(x) + b(x) = \frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2} = \frac{2f(x)}{2} = f(x)$ .

Next, since $a(-x) = \frac{f(-x)+f(x)}{2} = a(x)$ , we have that $a(x)$ is even.

Similarly, since $b(-x) = \frac{f(-x)-f(x)}{2} = -\frac{(f(x)-f(-x))}{2} = -b(x)$ , we have that $b(x)$ is odd. Thus, $f(x)$ can be expressed as the sum of an even function and an odd function.

Now, suppose $f(x)$ could written as the sum of an even and an odd function in two ways:

$f(x) = a_{1}(x) + b_{1}(x) = a_{2}(x) + b_{2}(x)$

A little algebra gives us

$a_{1}(x) - a_{2}(x) = b_{2}(x) - b_{1}(x)$

Since the sum of even functions is even and the sum of odd functions is odd, we have an even function, $a_{1}(x) - a_{2}(x)$ , equal to an odd function, $b_{2}(x) - b_{1}(x)$ . The only function that is both even and odd is the zero function (another fun proof!), therefore

$a_{1}(x) - a_{2}(x) = b_{2}(x) - b_{1}(x) = 0$

and so

$a_{1}(x) = a_{2}(x)$

$b_{1}(x) = b_{2}(x)$

Thus, this representation of $f(x)$ is unique. (Note: since 0 is both even and odd, we can consider $f(x) = f(x) + 0$ to be the unique decomposition in case $f(x)$ is itself even or odd.)

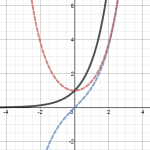
I was fortunate to encounter this unfamiliar fact at a time when hyperbolic trig functions were on my mind, which made it obvious to me where the hyperbolic sine and cosine functions come from: They are the even and odd parts of $e^x$ !

$e^x = \frac{e^{x} - e^{-x}}{2} + \frac{e^{x} + e^{-x}}{2} = sinh(x) + cosh(x)$

I also used this fact in a fun but inefficient proof that the derivative of an even function is an odd function.

Are there are other cool consequences of this unique decomposition of functions?

Related Posts

Derivatives of Even Functions

Categories: AppreciationGeometry

15 Comments

Graeme McRae · May 21, 2013 at 10:59 am

Thanks for posting this! I never thought of decomposing a function into odd and even parts before, and how naturally e^x is decomposed this way into sinh and cosh!

Sue VanHattum · May 21, 2013 at 11:25 am

I Love this idea. (Though I would change the word ‘factored’ in the third paragraph to something else – decomposed or split perhaps.)

What is intriguing me is that odd and even functions behave differently than odd and even numbers:
1. The zero function is both even and odd. (While the number zero is an even number.)
2. With numbers odd * odd = odd. With functions, odd * odd = even. This is because parity of functions is based on negatives, and – * – = +. I noticed this in calculus class a few weeks ago, and wanted to ponder it more. Your post provoked that pondering.

MrHonner · May 21, 2013 at 2:04 pm

Sue-

I had second thoughts about using “factor” in that context myself: it’s definitely an abuse of the term. I agree that “decompose” makes more sense, and I’ve made the change.

I’m glad that the idea has provoked some thought. What I’ve been thinking about lately is how the ideas of even and odd translate to functions of several variables.

Anonymous · June 2, 2013 at 2:46 pm

The difference between numbers and functions basically amounts to exponentiation. A power function x -> x^n is even or odd depending on whether n is even or odd. In other words, it’s what in the exponent that counts. Multiplying power functions amounts to adding the exponents, so we should expect multiplication of functions to behave like addition of numbers. Indeed it does: (odd function)*(odd function) = even function for the same reason as (odd number) + (odd number) = even number. Similarly, the multiplicative identity 1 is an even function, which corresponds to the fact that the additive identity 0 is an even number.

So the general rule is that (function, parity, multiplication, 1) corresponds to (number, parity, addition, 0), and then everything is perfectly parallel. Of course the fact that power functions work this way doesn’t prove anything in general, but it all works.

What about the zero function? There is no corresponding number, so the analogy tells us nothing here. Specifically, zero times anything is zero, so the analogue would be a number N such that N plus anything is N (maybe infinity?). If such an N did exist, then it would have to be both even and odd (since N+1=N), but it doesn’t exist. This is the same phenomenon as log(0) not being defined: 0 in addition corresponds to exp(0)=1 in multiplication, but you can’t reverse the process to find a number log(0) in addition that corresponds to 0 in multiplication.

MrHonner · June 4, 2013 at 7:44 pm

You’ve made some interesting points here, but of course there is much more to the universe of functions than just polynomials whose terms all have either even or odd degree. For example, y = (sin x)*(tan x) demonstrates the odd function * odd function = even function and there are no polynomials here, although I suppose one could always appeal to Taylor series!

Anam · August 11, 2013 at 3:11 pm

how we can decompose the function f(x)= x|x| into even and odd function

MrHonner · August 11, 2013 at 3:46 pm

Since f(x) = x|x| is an odd function itself, I suggest thinking of f(x) as f(x) + 0. Here, f(x) itself is the odd part and 0 is the even part.

Anam · August 11, 2013 at 3:13 pm

if there is a function which is neither even nor odd. If it so then why

MrHonner · August 11, 2013 at 3:48 pm

Certainly! You can easily construct polynomial functions that are neither even nor odd. Exponential functions, too, are neither even nor odd.

I suggest you head over to Desmos and play around!

Joshua · July 4, 2014 at 12:58 am

This sort of decomposition shows up in other places, too:
* Any square matrix can be written uniquely as a sum of a symmetric matrix and an anti-symmetric matrix.
* Any smooth map from the plane to itself can be written uniquely as a sum of a holomorphic function and an anti-holomorphic function.

Broadly speaking, if you have a vector space (such as a space of matrices or of functions), and a linear involution on that space (i.e., a map from the space to itself that is its own inverse, such as taking the transpose of a matrix or replacing f(x) with f(-x)), then any element of the space can be written uniquely as a sum of elements from the +1 eigenspace and the -1 eigenspace.

MrHonner · July 4, 2014 at 1:17 pm

Thanks for the comment, Joshua. Very enlightening, and lots for me to think about!

Joshua · July 5, 2014 at 11:44 am

I find this fact about even and odd functions fascinating, including the way it generalizes to lots of other situations just by thinking of it in terms of eigenspaces of a linear map. But I got overenthusiastic in talking about holomorphic and anti-holomorphic functions. (For instance, constant functions fall into both categories, which kills the possibility of uniqueness in the sum.)

What *is* true is that any linear map L from the plane to itself can be uniquely written as a sum L = A+B, where A is a complex-linear map (A(i*z) = i*A(z)) and B is a complex anti-linear map (B(i*z) = -i*B(z)). This means that the *derivative* of a smooth map from the plane to itself can be split into “z” and “z-bar” components, which is what I was going for.

MrHonner · October 22, 2014 at 6:44 am

John D. Cook recently posted a cool application of splitting a function into even and odd parts:

Integration Trick
http://www.johndcook.com/blog/2014/10/22/integration-trick/

Naseerah · February 25, 2016 at 1:40 pm

can we decompose a complex function into even and odd parts?

Jim Propp · August 20, 2016 at 9:37 pm

So far, commenters have discussed involutions (operations that bring you back to where you started after two applications), but variants of this decomposition theorem apply to other sorts of operations as well. For instance, any function of three variables (write it as f(x,y,z)) can be written in a unique fashion as a sum of two functions g and h such that for all x,y,z we have g(x,y,z) = g(y,z,x) = g(z,x,y) and h(x,y,z)+h(y,z,x)+h(z,x,y)=0. (Here the role formerly played by an involution is played by the operation of order three that cyclically permutes the coordinate axes.)