Teaching

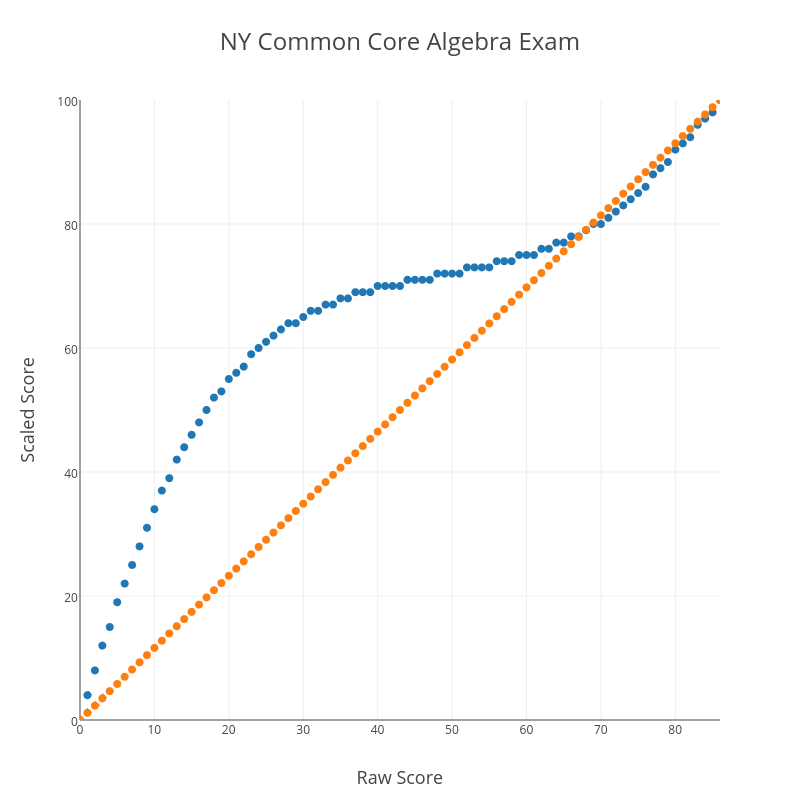
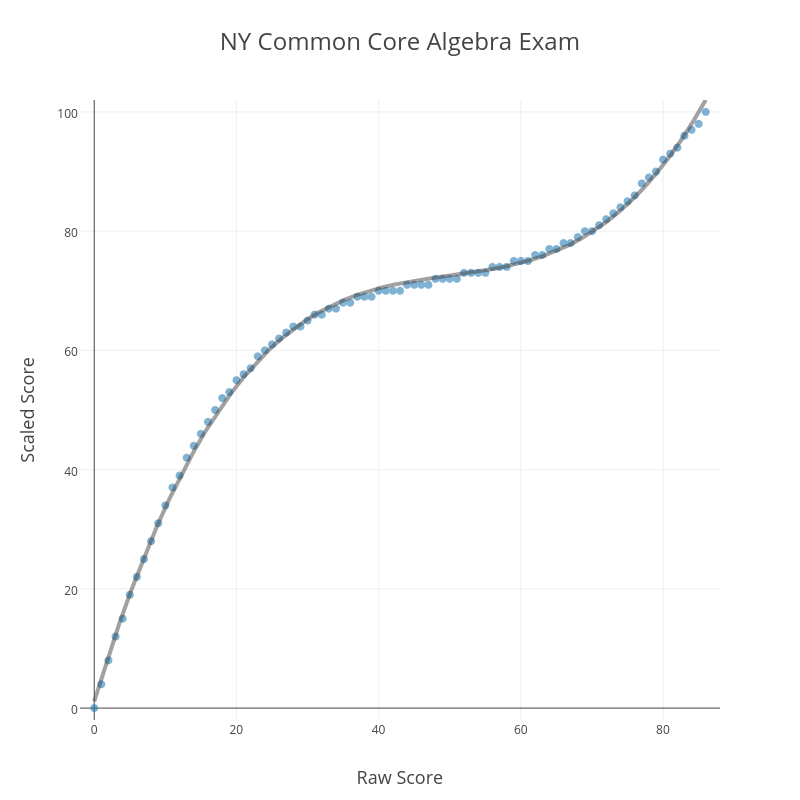
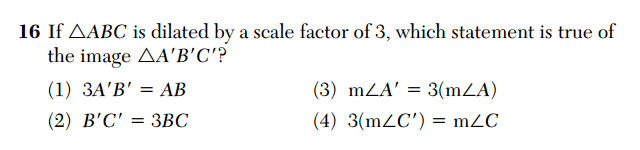Here is another installment in my series reviewing the NY State Regents exams in mathematics.

June, 2015 saw the administration of the first Common Core Geometry Regents exam in New York.  This exam will replace the Geometry Regents exam, which was also offered this testing cycle.

The CC Geometry exam has fewer multiple choice questions (24) than the Geometry exam (28).  It is worth noting that this change, in and of itself, likely will reduce average scores, as random guessing on those four extra questions would, on average, earn 2 points.  The free response sections are structured slightly differently, but not substantially so.  These differences mirror those between the new Common Core Algebra exam, introduced last year, and the old Integrated Algebra exam (see here).

The two Geometry exams are not drastically different, though there is greater emphasis on transformations on the CC Geometry exam, which I covered here.   However, there are some minor differences that have impact.

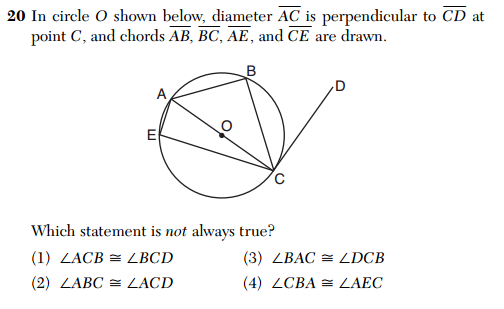
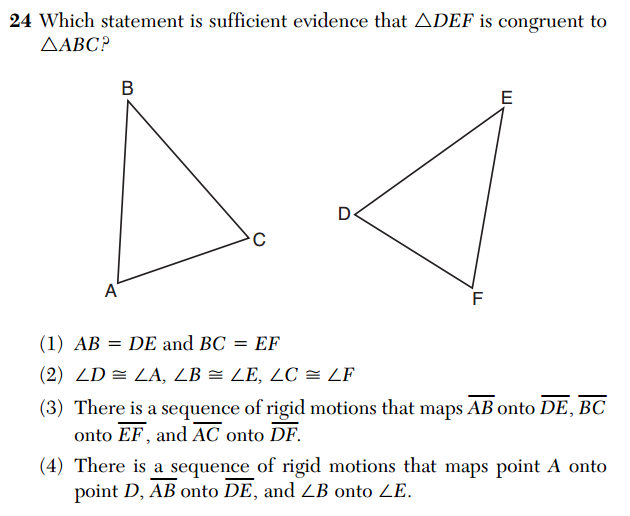
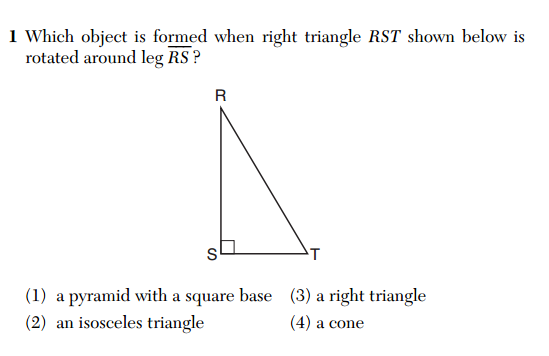
First, the multiple choice questions on the CC Geometry exam definitely seem a bit harder, on average, than those on the old Geometry exam.  One place this is apparent is the higher frequency of questions that ask the student to identify the false statement, rather than the true statement.  Here are two questions similar in content, one from each exam:  Question 20 from the CC exam (top) and Question 16 (bottom) from the non-CC exam.

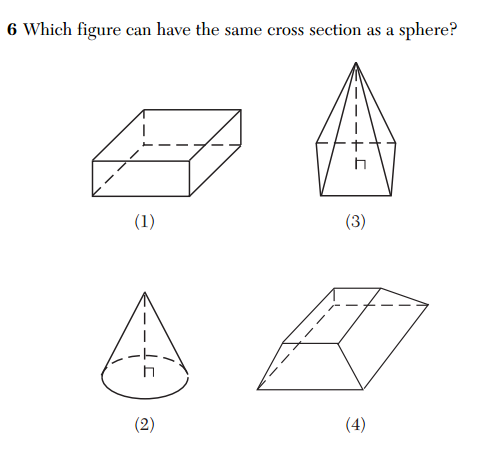
Generally speaking, I’d say it’s more challenging to identify a statement that is not always true than one which must be true.  There are three such problems on the CC exam, compared with one on the old exam.

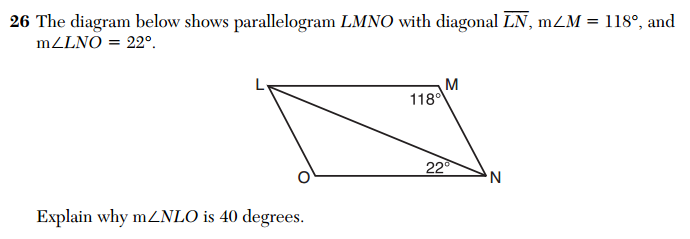
Question 26 on the CC exam exemplifies the increased emphasis on explaining one’s work.

A more traditional question might simply ask for the measure of angle NLO.  Here, the measure of the angle is given, and the student is asked to provide the mathematical justification for that value.

Lastly, our teacher team was somewhat surprised at how closely the exam tracked the sample items that were released by the state.  For example, the segment partitioning problem on the CC Geometry exam

was very similar to a sample item

Additionally, the construction problem on the CC Geometry exam

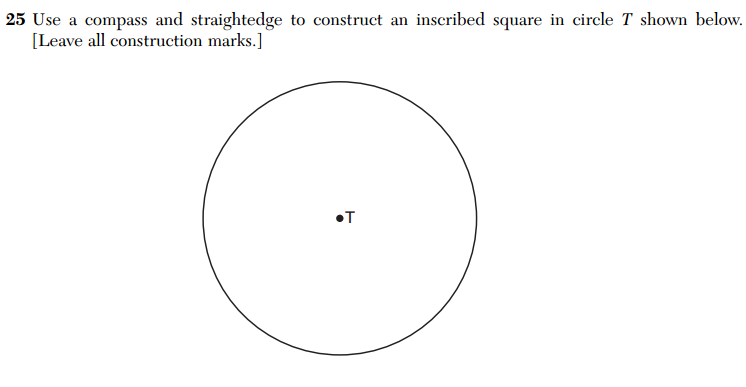was identical to problem 12 in the Fall sample items.

Our Geometry teacher team generally found this inaugural CC Geometry exam to be in line with our expectations in terms of content and difficulty.  If anything, we were surprised at how unsurprising it was to us.

More the anything related to the Common Core exam, the level of difficulty of the old Geometry exam given during the same cycle surprised us.  The multiple choice section seemed to be more challenging than those of past recent exams, which made us wonder if the two exams drew their multiple choice questions from a single pool.

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

June, 2015, saw the administration of the first Common Core Geometry Regents exam in New York.  I led a teacher team that worked to adapt our curriculum to the Common Core standards.  One of our primary concerns was how the new transformation-based approach to Geometry inherent in the Common Core standards would be represented on this Regents exam.  In particular, we had no idea how establishing congruence and similarity via transformations, an apparent emphasis of the standards, would be assessed.

A total of 18 of the 86 points on the exam (around 21%) were associated with transformations:  six multiple choice questions and two free response questions.  Here are a few examples, with associated Common Core standards in parentheses.

Question 10 is about rotations that map regular polygons onto themselves (CCSS.MATH.CONTENT.HSG.CO.A.3).

Question 16 assesses the concept that dilation can alter length but must preserve angle measure (CCSS.MATH.CONTENT.HSG.SRT.B.5).

Question 24 addresses establishing congruence by rigid motions (CCSS.MATH.CONTENT.HSG.CO.B.7).

Question 30 asks the student to explicitly connect transformations to congruence by recalling the fundamental principles that underlie rigid motions (CCSS.MATH.CONTENT.HSG.CO.B.6).

And Question 33 asks to student to first produce a “traditional” proof of congruence, and then interpret the congruence through a rigid motion (CCSS.MATH.CONTENT.HSG.CO.C.11).  This is a simple way to connect the two concepts.

Overall, the manner in which transformations were tested aligned with our expectations, both in scope and in content.  Our Geometry worked closely together throughout the year, integrating a variety of resources from New York state and elsewhere, but mostly felt in the dark about what the test would look like.  In the end, we were pleasantly surprised.  But we also noticed how much different the Common Core Algebra exam was in year two, so we know that we may be surprised again.

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

The Common Core standards have brought a slight increase in three dimensional reasoning into high school Geometry.  I think this is generally a good thing:  3D geometry is typically given short shrift in this course, but is a beautiful and intriguing topic.

It can also be a confusing topic, as these problems from the inaugural Common Core Geometry Regents exam demonstrate.

According to the scoring guide, the correct answer is (4) a cone.  Technically, however, the correct answer is (3) a right triangle.

Rotation is a rigid motion:  it does not change a figure’s size or shape.  If a right triangle is rotated about an axis, it will remain a right triangle.  Presumably, the intent of this question is for the student to identify the solid of revolution formed by revolving the triangle about an axis.  But that is a different question than the one posed.  Ironically, the notion that rigid motions preserve size and shape is one of the fundamental principles in the transformation-based approach to geometry embodied by the Common Core standards.

Here’s another problematic 3D geometry question.

According to the answer key, the correct answer is (2).  But the actual correct answer is all of these.  While most cross-sections of spheres are circles, some cross-sections of spheres are single points (when the cross-sectional plane is tangent to the sphere).  All the given objects have single point cross-sections as well, thus, could all have the same cross section as a sphere.

This is certainly not the first time we’ve seen problematic three dimensional geometry questions on these Regents exams (here’s a particularly embarrassing example), and I’ve been chronicling mathematically erroneous questions on these tests for years.  Errors like this are often dismissed as insignificant, or “typos”, but because of the high-stakes nature of these exams, these errors have real consequences for students and teachers.

If these exams don’t model exemplary mathematics and mathematical practice, their credibility in evaluating the mathematical practice of students and teachers must be questioned.