patrick honner

Math teacher in Brooklyn, New York

NBA Draft Math: Strength of Draft Class

After creating a simple metric to evaluate the success of an NBA draft pick, I realized that the same approach could be used to evaluate the overall strength of a draft class.

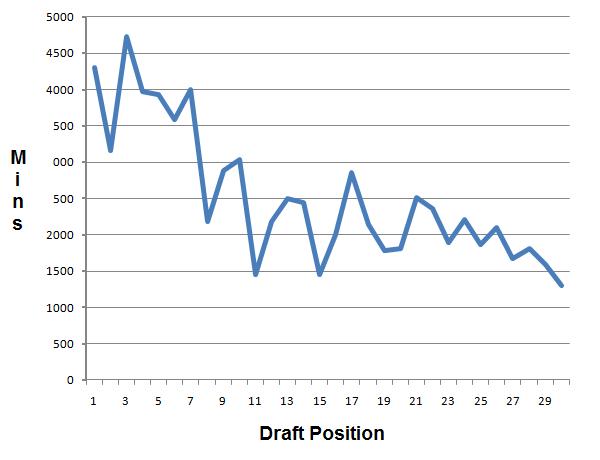
To quantify the success of an individual draft pick I’m looking at the total minutes played by a player during the first two years of his contract.  As far as simple evaluations are concerned, I think minutes played is as good a measure as any of a player’s value to a team, and I’m only looking at the first two years as those are the only guaranteed years on a rookie’s contract.  This is by no means a thorough measure of value–it’s meant to be simple while still being relevant.

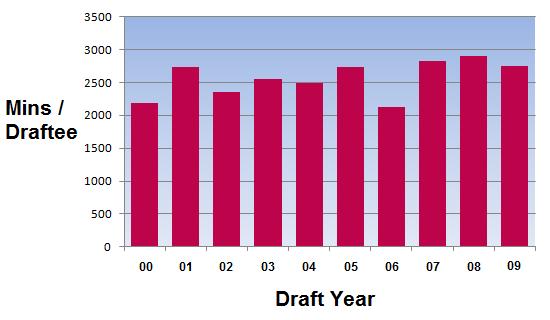
After using this measure to compare the performance of individual draft picks, I used the same strategy to evaluate the entire “Draft class”.  I computed the average total minutes per player for the entire first round (picks 1 through 30, in most cases) of each draft from 2000 to 2009.  Here are the results.

There doesn’t seem to be much variation among the draft classes, but the 2006 draft certainly looks weak by this measure.  Upon closer inspection, that year does seem like a weak draft:  the best players being LeMarcus Aldridge (2), Brandon Roy (6), and Rajon Rondo (21).  The weakness of the 2000 draft also seems reasonable upon closer inspection at basketball-reference.com.

Another approach would  be to somehow aggregate the career stats of each player in a draft, rather than looking at only the first two years, but that would make it difficult to compare younger and older players.

Are there any other suggestions for rating the overall strength of an NBA draft class?

Related Posts

 

By patrick honner, ago

NBA Draft Math, Part I

Having put some thought into the mathematics of the NFL draft, I decided to turn my attention to basketball.  From an anecdotal perspective, the NBA draft seems to be more hit-or-miss than the NFL draft:  teams occasionally have success and draft a great player, but it seems more common that a draft pick doesn’t achieve success in the league.

In an attempt to quantify the “success” of an NBA draft pick, I researched some data and ending with choosing a very simple data point:  the total minutes played by the draft pick in their first two seasons.

Total minutes played seems like a reasonable measure of the value a player provides a team:  if a player is on the floor, then that player is providing value, and the more time on the floor, the more value.  I looked only at the first two seasons because rookie contracts are guaranteed for two years; after that, the player could be cut although most are re-signed.  In any event, it creates a standard window in which to compare.

There are plenty of shortcomings of this analysis, but I tried to strike a balance between simplicity and relevance with these choices.

I looked at data from the first round of the NBA draft between 2000 and 2009.  For each pick, I computed their total minutes played in their first two years.  I then found the average total minutes played per pick over those ten drafts.

Not surprisingly, the average total minutes played generally drops as the draft position increases.  If better players are drafted earlier, then they’ll probably play more.  In addition, weaker teams tend to draft higher, and weak teams likely have lots of minutes to give to new players.  A stronger team picks later in the draft, in theory drafts a weaker player, and probably has fewer minutes to offer that player.

However, when I looked at the standard deviation of the above data, I found something more interesting.  Standard deviation is a measure of dispersion of data:  the higher the deviation, the farther data is from the mean.

Notice that the deviation, although jagged, seems to bounce around a horizontal line.  In short, the deviation doesn’t decrease as the average (above in blue) decreases.

If the total number of minutes played decreases with draft position, we would expect the data to tighten up a bit around that number.  The fact that it isn’t tightening up suggests that there are lots of lower picks who play big minutes for their teams.  This might be an indication that value in the draft, rather than heavily weighted at the top, is distributed more evenly than one might think

This rudimentary analysis has its shortcomings, to be sure, but it does suggest some interesting questions for further investigation.

Related Posts

By patrick honner, ago

The Write Angle for Teaching Math: Keys to Success

Math WritingFinding ways to get students to write about mathematics has played a pivotal role in my development and growth as a math teacher.  Mathematical writing challenges students to express their ideas clearly and efficiently; it forces students to stop thinking of mathematics as merely equations and answers; and it opens up a new and unexpected dialogue between math teacher and student.

I have always found great value and pleasure in writing.  It is a valuable skill, a necessary tool of scholarship, and a powerful creative outlet.  And now I see its value as a math teacher.  The more my students write, the more useful and interesting we all find it.

In this post, I’ll discuss some strategies for making writing part of the culture of the math classroom.

Here are a few simple things that make writing in math class work for me and my students.

Keys to Success

1)  Short and Sweet

Keep the assignments short and well-defined, especially at the beginning.  Don’t ask students to write pages and pages; sometimes a short paragraph or even a thoughtful sentence says it all!  Students may be hesitant to write at first, so making it easy on them can help get the process moving.

2)  Feedback

As with all student work, meaningful feedback goes a long way.  Make sure the students know that you are reading their work, even if you aren’t grading everything.  Correct as much grammar as you are comfortable with, but don’t necessarily feel obligated to grade it like a literature teacher might.  This is likely to be an “extra” assignment anyway, for both the students and you!  Keep it fun.

3)  Shareout and Peer Review

With every assignment, honor those pieces that really moved you by picking a few and sharing them with the class.  Have small groups exchange papers and then share their favorites aloud.  It only takes a few minutes, but sharing rewards students for taking a risk in their writing, and regular peer review helps everyone get better over time.

Get Writing!

There are a lot of ways to get students writing in math class.  It isn’t easy, and it takes time for everyone to get comfortable with it, but it’s an investment worth making.  Establishing a culture of writing has dramatically impacted my classroom:  it gives my students a different way to interact with mathematics, and it gives me a different look into how my students think about math.

For more resources, see my Writing in Math Class page.

By patrick honner, ago

Fun With Self-Referential Tests

A few years ago, I stumbled upon James Propp’s Self-Referential Aptitude Test.  I was immediately hooked, and spent hours navigating the interconnected logic puzzle that posed questions like “The answer to number 8 is ” and “The first question whose answer is C is “.

The experience was so challenging, frustrating, and ultimately rewarding, that it didn’t take long to realize it was a perfect exercise for students.

I ended up creating some simpler examples that gently introduce the student to the idea of a self-referential test, a test where questions and answers refer to other questions and answers.  By playing around with these easier versions, students develop a sense of how to reason their way through using various problem-solving strategies.

After working through the more challenging versions, the final project for students is to create their own self-referential tests, which we then all enjoy solving.  This is the perfect kind of project, in that it allows students to exercise their creativity while pondering substantial and significant mathematical questions like “What constitutes a solution to this test?” and “Are we sure that this puzzle has a solution?”, as well as fundamental mathematical ideas like logical consistency.

To get you started, I offer two simple versions of the test.

Five Question version: Simple Self-Referential Test 1

Ten Question version: Simple Self-Referential Test 2

Enjoy!  And if you do, try making your own!  It’s great fun, and a great student project.  And keep in mind, questions like “Does this test have a solution?” and “Does this test have a unique solution?” are always interesting to consider.

And you can find James Propp’s original Self-Referential Aptitude Test here.  Be warned:  you might find it very frustrating!

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: