patrick honner

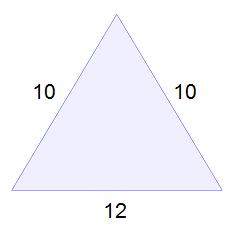
As it’s 10/12/10, I thought it would be the appropriate day to appreciate the 10-10-12 triangle!

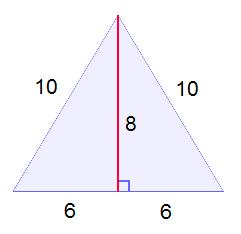
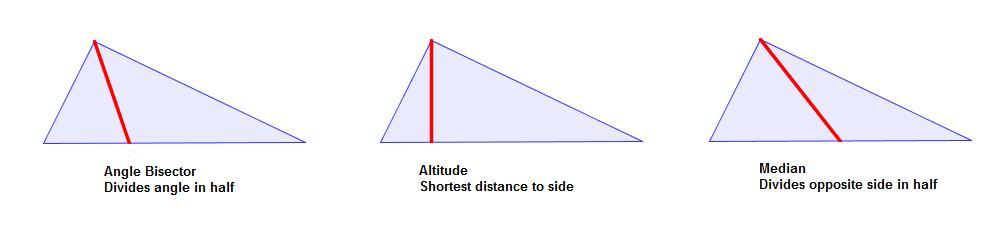
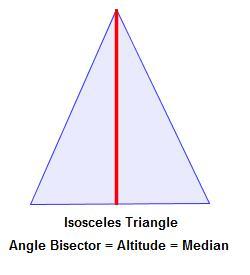
Of course, it’s nice that the 10-10-12 triangle is isosceles.  But what’s really cool is what happens when you drop the altitude from the top vertex!

It’s well known that in an isosceles triangle, the median and the altitude from the vertex are the same–this means that not only does this segment make a right angle (it’s the altitude), but it also divides the opposite side at its midpoint (it’s the median).  So that segment creates two right triangles with hypotenuse 10 and side 6.  Of course, the other side must be eight, since

Thank you, Pythagorean Theorem.  So the 10-10-12 triangle is just two right triangles pasted together.

It’s not quite equilateral, but the 10-10-12 triangle is still pretty cool.

Related Posts

• Ode to Equilateralism
• More Triangle Appreciation
• The Final Word in Triangle Appreciation

Today, 10/10/10, is Equilateral Triangle Day!  This day doesn’t come around that often, so I thought I’d expound a bit on the virtues of equilateralism.

There is so much to appreciate about the equilateral triangle–its uniform shape, its simple area formula, its presence in regular hexagons, its decomposition into 30-60-90 triangles–and most of these properties are a consequence of the equilateral triangle’s abundance of symmtery.

Consider this plain old non-equilateral triangle.

In any triangle, from any vertex there are three important segments you can draw–the angle bisector, the altitude, and the median.  Each of the segments defines a kind of symmetry for that part of the triangle.

Notice how these three segments are all quite different in our plain old non-equilateral triangle.  But, if we were to make the two sides from that vertex the same length (i.e., make the triangle isosceles), all those segments become equal!

The sides being the same length force all those lines of symmetry to become one.  Now, the beauty of the equilateral triangle is that it’s like three isosceles triangles rolled into one! 

It’s an isosceles triangle from every vertex!  So, all those lines of symmetry are the same no matter how you look at it.

Enjoy the next 397 days, until the next Equilateral Triangle Day.

Related Posts

• 11/11/11 — Equilateral Triangle Day
• 12/12/12 — Equilateral Triangle Day
• Which Triangle is More Equilateral?