11/11/11 — Equilateral Triangle Day!

Published by patrick honner on November 11, 2011November 11, 2011

While others celebrate the number 11 on this special day, I prefer to honor the Equilateral Triangle.

Last year, on 10/10/10, I celebrated the symmetry of the equilateral triangle. This year, I offer a favorite Proof Without Words. Well, a proof with some words. In any event, we will use equilateral triangles to prove that the following infinite series

$\frac{1}{4}$ + $\frac{1}{16}$ + $\frac{1}{64}$ + $\frac{1}{256}$ + . . .

is $\frac{1}{3}$ .

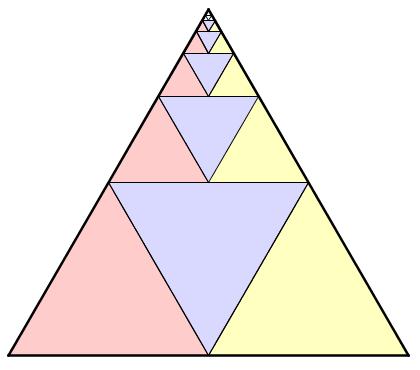
Consider the following diagram.

Notice that the largest blue equilateral triangle is $\frac{1}{4}$ the area of the entire equilateral triangle. The next largest blue triangle is $\frac{1}{4}$ of $\frac{1}{4}$ , or $\frac{1}{16}$ of the entire triangle. The next largest blue triangle is $\frac{1}{64}$ of the original triangle, and so on.

So, the sum of the blue triangles is

$\frac{1}{4}$ + $\frac{1}{16}$ + $\frac{1}{64}$ + $\frac{1}{256}$ + . . .

Let’s call this S.

Now, here’s the magic: the sum of the red triangles is also S! This is true because for every blue triangle, there is a congruent red triangle right next to it. Similarly, the sum of the yellow triangle is also S.

When you put all the blue, red, and yellow triangles together, you get the original triangle, whose area is 1. Thus, 3S = 1, and so

$S = \frac{1}{3}$

Therefore, we have

$\frac{1}{4}$ + $\frac{1}{16}$ + $\frac{1}{64}$ + $\frac{1}{256}$ + . . . = $\frac{1}{3}$

Happy Equilateral Triangle Day!

Related Posts

5 Comments

Whered · November 11, 2011 at 9:32 am

What about Veteran’s day?

MrHonner · November 11, 2011 at 9:45 am

I recognize Armistice Day, but the mathematics that naturally comes to mind (total losses due to war) is too much of a downer to write about.

janinelson (@janinelson) · November 11, 2011 at 9:37 am

Thanks… I love this one… only wish we were in school today– I would use it with my students!! Oh well, guess I will need to wait until next year 12/12/12

MrHonner · November 11, 2011 at 9:46 am

I love this one, too–a student showed this to me last year.

And make sure to use it on 12/12/12! Otherwise, you’ll be waiting a long time for the next opportunity.

chrisharrow · November 11, 2011 at 10:49 am

I think the image is gorgeous as a proof without words.