Dan Meyer recently shared a fun and telling graph describing his year in math. Inspired by Dan’s idea, and by a Math for America workshop with data visualization innovator Mona Chalabi, I created my own Year in Math entry. Though the real inspiration, I guess, came from the world events that made me want to read more books and less internet.
You can find more takes on the Year in Math theme on Twitter.
I think this could make for a fun student project. I hope the students agree!
My latest column for Quanta Magazine is about the recent classification of pentagonal tilings of the plane. Tilings involving triangles, quadrilaterals, and more have been well-understood for over a thousand years, but it wasn’t until 2017 that the question of which pentagons tile the plane was completely settled.
Here’s an excerpt.
People have been studying how to fit shapes together to make toys, floors, walls and art — and to understand the mathematics behind such patterns — for thousands of years. But it was only this year that we finally settled the question of how five-sided polygons “tile the plane.” Why did pentagons pose such a big problem for so long?
In my column I explore some of the reasons that certain kinds of pentagons might, or might not, tile the plane. It’s a fun exercise in elementary geometry, and a glimpse into a complex world of geometric relationships.
The full article is freely available here.
Today we celebrate a Permutation Day! I call days like today permutation days because the digits of the day and the month can be rearranged to form the year.
Celebrate Permutation Day by mixing things up! Try doing things in a different order today. Just remember, for some operations, order definitely matters!
My latest piece for the New York Times Learning Network gets students investigating the mathematics of gerrymandering. Through applying geometry, proportionality, and the efficiency gap, students explore the notion of a “workable standard” for identifying and evaluating biased electoral maps.
Here is an excerpt:
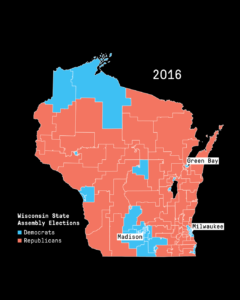
Math lies at the heart of gerrymandering, in which the shapes of voting districts and distributions of voters are manipulated to preserve and expand political power.
The strategy of gerrymandering is not new… However, new, sophisticated mathematical and computer mapping tools have made gerrymandering an even more powerful way to tilt the playing field. In many states, where the majority party has the authority to rewrite the electoral map, legislators essentially have the power to choose their voters — to create districts in any shape or size that will weaken their opponents and increase their dominance.
In this lesson, we help students uncover the mathematics behind these biased electoral maps. And, we help them apply their mathematical knowledge to identify and address the problem.
In fact, the questions students will work through are similar to those the Supreme Court is now considering on whether gerrymandering can ever be declared unconstitutional.
The article was co-authored with Michael Gonchar of the NYT Learning Network, and is freely available here.
Related Posts
These cacti caught my. I can see both a dodecagon and a star in the 12-fold symmetry of the cactus in front. And to my surprise, the cactus behind it has thirteen sections!
I wonder about the range, and deviation, of the number of sections of these cacti. And what are the biological principles that govern these mathematical characteristics?