Benoit Mandelbrot died this week at the age of 85, leaving a giant mark on the worlds of mathematics and science. Mandelbrot coined the term fractal, writing the seminal book on the topic in 1982–The Fractal Geometry of Nature. By rejecting the generally accepted, if never actually articulated, notion that things were smooth, Mandelbrot challenged everyone’s notion of shape, distance, and dimension.
Benoit Mandelbrot died this week at the age of 85, leaving a giant mark on the worlds of mathematics and science. Mandelbrot coined the term fractal, writing the seminal book on the topic in 1982–The Fractal Geometry of Nature. By rejecting the generally accepted, if never actually articulated, notion that things were smooth, Mandelbrot challenged everyone’s notion of shape, distance, and dimension.
As is often the case, Mandelbrot was considered crazy at first, but he dies with almost legendary status. We will likely be talking about fractals and Mandelbrot sets hundreds if not thousands of years from now, the way we talk about the Pythagorean Theorem and Euler’s Number today.
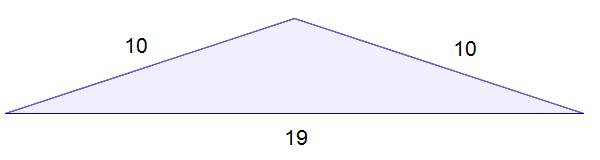
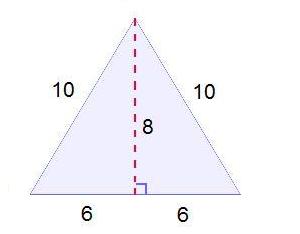
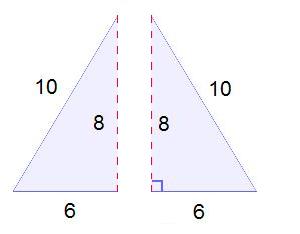
And as is also often the case, Mandelbrot’s brilliant and revolutionary ideas can be traced to a simple question that he chose to think of differently: how long is the coast of Britain?
The answer, he was surprised to discover, depends on how closely one looks. On a map an island may appear smooth, but zooming in will reveal jagged edges that add up to a longer coast. Zooming in further will reveal even more coastline.
“Here is a question, a staple of grade-school geometry that, if you think about it, is impossible,” Dr. Mandelbrot told The New York Times earlier this year in an interview. “The length of the coastline, in a sense, is infinite.”
From Mandelbrot’s NYT’s obituary.
 I am very excited to have my first Lesson Plan published by the New York Times Learning Network. I wrote a mathematics lesson built around profiling the upcoming presidenital election, using data and analysis from Nate Silver’s 538 Blog at the Times.
I am very excited to have my first Lesson Plan published by the New York Times Learning Network. I wrote a mathematics lesson built around profiling the upcoming presidenital election, using data and analysis from Nate Silver’s 538 Blog at the Times.