March 2018

sin(x) + cos(x)

Here is a fun little exploration involving a simple sum of trigonometric functions.

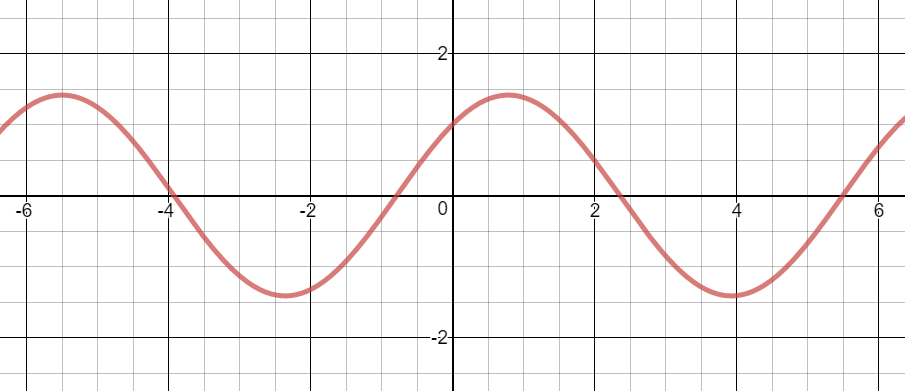
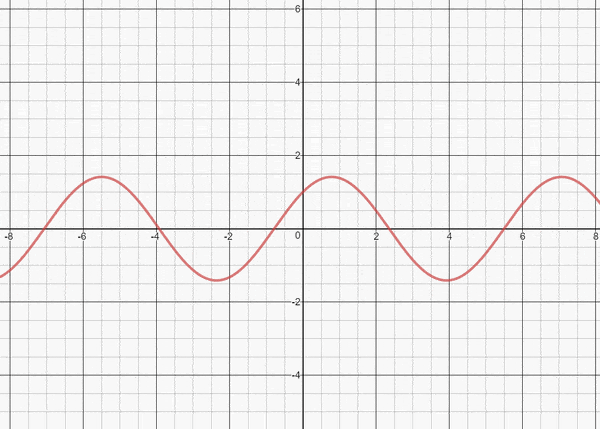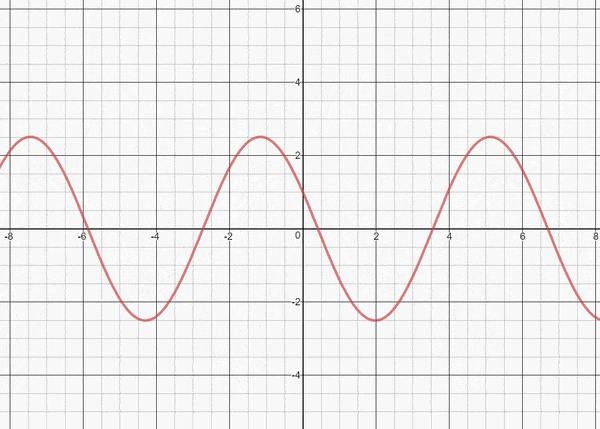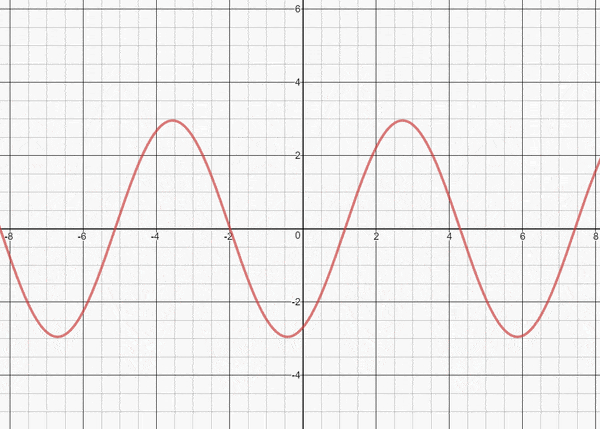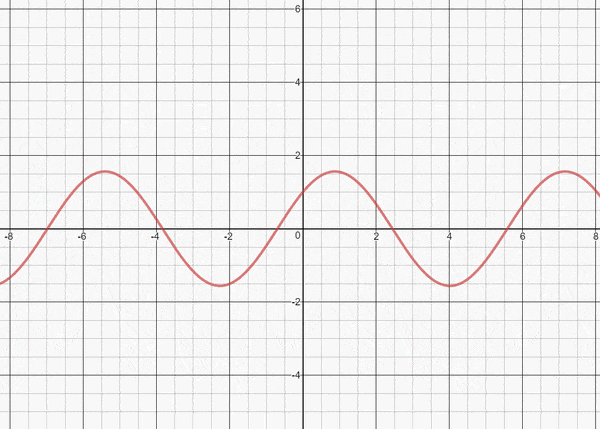
Consider f(x) = sin(x) + cos(x), graphed below.

Surprisingly, it appears as though sin(x) + cos(x) is itself a sine function. And while its period is the same as sin(x), its amplitude has changed and it’s been phase-shifted. Figuring out the exact amplitude and phase shift is fun, and it’s also part of a deeper phenomenon to explore.

Consider the function g(x) = a sin(x) + b cos(x). Playing around with the values of a and b is a great way to explore the situation.

On the way to a complete solution, a nice challenge is to find (and characterize) the values of a and b that make the amplitude of g(x) equal to one. It’s also fun to look for values of a and b that yield integer amplitudes: for example, 5sin(x) + 12cos(x) has amplitude 13, and 4sin(x) + 3cos(x) has amplitude 5.

Ultimately, this exploration leads to a really lovely application of angle sum formulas. Recall that

sin(A + B) = sin(A) cos (B) + sin(B) cos(A)

If we let A = x, we get

sin(x + B) = sin(x) cos(B) + sin(B) cos(x)

With a little rewriting, we have

sin(x + B) = cos(B) sin(x) + sin(B) cos(x)

which looks similar to our original function f(x) = sin(x) + cos(x), except for what’s in front of sin(x) and cos(x). We handle that with a clever choice of B.

Let B = \frac{\pi}{4}. Now we have

sin(x + \frac{\pi}{4}) = cos(\frac{\pi}{4})sin(x) + sin(\frac{\pi}{4})cos(x)

sin(x + \frac{\pi}{4}) = \frac{\sqrt{2}}{2} sin(x) + \frac{\sqrt{2}}{2}cos(x)

And a little algebra gets us

sin(x) + cos(x) = \sqrt{2}sin(x + \frac{\pi}{4})

And so sin(x) + cos(x) really is a sine function! Not only does this transformation explain the amplitude and phase shift of sin(x) + cos(x), it generalizes beautifully.

For example, consider 5sin(x) + 12cos(x). We can rewrite this in the following way.

5sin(x) + 12cos(x) = 13 ( \frac{5}{13} sin(x) + \frac{12}{13} cos(x))

5sin(x) + 12cos(x)= 13 ( cos(\beta) sin(x) + sin(\beta) cos(x))

5sinx + 12cosx = 13 sin (x + \beta)

where \beta = arcsin(\frac{12}{13}) = arccos(\frac{5}{13}).

There’s quite a lot of trigonometric fun packed into this little sum. And there’s still more to do, like exploring different phase shifts and trying the cosine angle sum formula instead. Enjoy!

Related Posts

 

By MrHonner, ago

Forbes Feature

Following up on my appearance on the My Favorite Theorem podcast, co-host Kevin Knudson has an article in Forbes about Varignon’s Theorem, the topic of my episode. Kevin recaps some of the ideas we discussed, including my favorite proof of my favorite theorem.

You can read the article here, and catch the full podcast episode on Kevin’s website.

Related Posts

By MrHonner, ago

Regents Recap — January, 2018: Problems with Pre-Calculus

Since the advent of the “Common Core” Regents exams in New York state, there has been a noticeable increase in decidedly Pre-Calculus content on the tests. Questions involving rates of change, piecewise functions, and relative extrema now routinely appear on the Algebra I and Algebra II exams. Unfortunately, these questions also routinely demonstrate a disturbing lack of content knowledge on the part of the exam creators.

Here’s number 36 from the January, 2018 Common Core Algebra I Regents exam.

This graph represents “the number of pairs of shoes sold each hour over a 14-hour time period” by an online shoe vendor. A simple enough start. But things start to get tricky halfway down the page, when the following directive is issued.

State the entire interval for which the number of shoes sold is increasing.

The answer must be 0 < t < 6, because that’s when the graph is increasing, right? The official rubric says so, and the Model Response Set backs it up (this Model Response has been edited to show only the portion currently under discussion).

But 0 < t < 6 is not the correct answer. Can you spot the wrinkle here? Basically, the number of shoes sold is always increasing.

The graph shown is a model of the number of shoes sold per hour. The model shows that, at any time between t = 0 and t = 14, a positive number of shoes are being sold per hour. In short, more shoes are always being sold. That means the number of shoes sold is always increasing. The correct answer is 0 < t < 14.

The exam creators have made a conceptual error familiar to any Calculus teacher: they are conflating a function and its rate of change.

In this problem, the directive pertains to the number of shoes sold. But the given graph shows the rate of change of the number of shoes sold. The given graph is indeed increasing for 0 < t < 6, but the question isn’t “When is the rate of change of shoes sold increasing?” The question is “When is the number of shoes sold increasing?” Since a function is increasing when its rate of change is positive, this means the number of shoes sold is increasing whenever the graph is positive. Thus, the answer is 0 < t < 14.

After the exam was given and graded, those in charge of the Regents exams became aware of the error. They quickly issued a correction, updated the rubric, and instructed schools to re-score the question (giving full credit for either 0 < t < 6 or 0 < t < 14). Thankfully, it didn’t take a change.org campaign and national media attention for them to admit their error.

But as usual, they did their best to dodge responsibility.

In their official correction, the exam creators blamed the issue on imprecision in wording, pretending that this was just a misunderstanding, rather than an embarrassing mathematical error. This is something they’ve done over and over and over again. These aren’t typos, miscommunications, or inconsistencies in notation. These are serious, avoidable mathematical errors that call into question the validity of the very process by which these exams are constructed, graded, and, ultimately, used. We all deserve better.

Related Posts

 

By MrHonner, ago

My PAEMST Story

My heart sank a little as I watched the video.

It had been three months since I submitted my application for the Presidential Award for Excellence in Mathematics and Science Teaching (PAEMST). As I often do in the summer, I was reviewing materials from the school year, cleaning up and getting organized. I found my PAEMST application folder, noticed the video — the centerpiece of the application portfolio — and clicked play.

I remembered feeling pretty good about the lesson I chose to record. Re-watching it months later confirmed that it was a good lesson. But it wasn’t flashy. I didn’t perform a rap about even and odd functions. Students weren’t chasing each other around the classroom in a relay race. I didn’t dramatically slice a melon in half with a meat cleaver. My chance of earning the country’s highest honor for K-12 STEM teachers hinged on this video, but it was just me teaching a normal lesson. I resigned myself to the fact that my odds probably weren’t very good.

But as I continued to watch the video, my attitude slowly changed. No, it wasn’t flashy — my lessons never are — but it was a really good lesson. It was well-designed, well-executed, and well-received. Students were deeply engaged in complex mathematics. There was a clear arc that everyone could connect with. By the end of the video, my resignation had turned to pride: This is what happens every day in our classroom. This is who I am as a teacher. This was a normal day: exactly the right way to represent myself and my work.

I know what kind of teaching captures the public’s interest, and this wasn’t it. But I was proud of what was showcased in the video, even if it might not look like “great teaching” to an outside observer. Would PAEMST reviewers appreciate the well-chosen problems that bridged prior knowledge and new concepts? Would they notice the classroom culture in which students immediately began collaborating, seeking each other’s validation before mine? Would they see the subtle changes I made after assessing small group discussions? Would they appreciate how I strategically answered some questions and respectfully put others right back to the students? Would they notice how students listened to each other during whole-class discussion? How they comfortably responded to each other’s questions? How they made conjectures that would be resolved later in the lesson?

I guess they did.

I received the Presidential Award in 2013. Here I am, between then-US CTO Megan Smith and Dr. France Cordova, Director of the National Science Foundation. It was a tremendous honor to win the PAEMST and to travel to Washington D.C. to meet leaders from the National Science Foundation, the National Academy of Sciences, and the White House. And meeting and connecting with other awardees — teachers doing great work in all manners of classrooms, schools, and communities across the country — continues to impact the work I do.

And it was encouraging to know that those responsible for awarding the PAEMST understood what they were looking at when they watched my video: nothing flashy, just good teaching. The kind that happens in my classroom, and countless others around the country, every day. Years later, I still occasionally look at my PAEMST application materials: the essays, the artifacts, even the video. It’s a nice snapshot of where I was at in 2013, and it’s fun and productive to think about the ways I’ve changed, and stayed the same, as a teacher.

Creating that snapshot is one of the many reasons I encourage teachers to apply for the PAEMST. The application process is a worthwhile professional experience in and of itself. It’s the kind of work good teachers want to do anyway: planning instruction; thinking about curriculum; analyzing outcomes; reflecting on process. Applying for the Presidential Award is a great motivator to do that work.

Teachers out there who feel ready should consider applying. And if you know a great teacher, you can nominate them for the Presidential Award. The process alone is worth it, and the potential reward is career-changing.

Related Posts

By MrHonner, ago

AMS Feature

My latest column for Quanta Magazine, on vaccinations and the mathematics of herd immunity, was the subject of a recent feature on the American Mathematical Society’s website. I also answer a few questions, including one about the challenges of communicating mathematics to those who may be reluctant to listen.

“I’d say the more we can get people to tap into their inner mathematicians and inner scientists, the better. As a teacher, I’m always trying to get students to engage actively with mathematical ideas, and not just simply consume mathematical results. In some ways, I think this applies to communication and outreach, too”

You can read the full piece here.

Related Posts

 

By MrHonner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: