Fun With a Favorite Triangle

In a post examining the quality of New York State Math Regents exams, I considered the following problem from the 2011 Algebra 2 / Trigonometry exam:

In triangle ABC, we have a = 15, b = 14, and c = 13.  Find the measure of angle C.

This problem is designed to test the student’s knowledge of the Law of Cosines.  The Law of Cosines is an equation relating the three sides and one angle of the triangle; knowledge of any three of those four quantities allows you to determine the fourth.  Substitute the three sides into the equation, perform some algebra and simple trigonometry, and you’ll get the angle.

This isn’t just any triangle, though:  this is the famous 13-14-15 triangle.  The 13-14-15 triangle has some special properties that allow you to solve this problem without using the Law of Cosines!

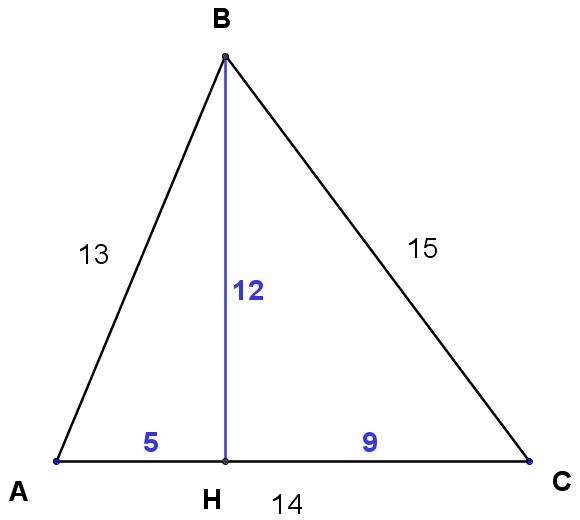
For example, when you drop the altitude the side of length 14, something amazing happens.

Altitudes are perpendicular to bases, so two applications of the Pythagorean Theorem and a little algebra show that the foot of the altitude, H, divides AC into segments of length 5 and 9.  This means that triangle AHB is a right triangle with sides 5, 12, and 13 and triangle CHB is a right triangle with sides 9, 12, and 15.  As it turns out, our 13-14-15 triangle is just two famous right triangles glued together along a common side!

This makes finding the measure of angle C easy:  since C is an angle in a known right triangle, just use right triangle trigonometry!  Much easier than using the Law of Cosines.

And for the record, this was a multiple choice question.  A clever student had yet another opportunity to eschew the Law of Cosines.

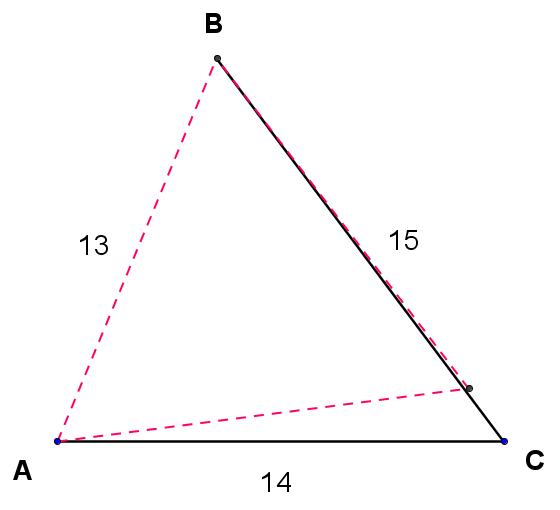
In any triangle, the smallest angle is opposite the shortest side.  This allows us to immediately conclude that angle C is less than 60 degrees and thereby eliminate two of the four answer choices, 67 and 127.  Similarly, the longest side of a triangle is opposite the largest angle, which means that angle A is greater than 60 degrees.  Using a straight-edge and compass, we can construct the following equilateral triangle with side AB.

The two remaining choices for the measure of angle C are 53 and 59.  Our diagram suggests that angle B is very close to 60 degrees.  Since A is bigger than 60 degrees, C must be less than 60 degrees by roughly that same amount.  So the question is now ‘Is the measure of angle A 7 degrees more than 60, or 1 degree more than 60?”.  If the diagram is to scale (mine is; I’m not sure about the diagram included in the Regents exam), a 7-degree difference seems more likely.  It’s admittedly not a rigorous solution, but it’s not a bad way to navigate to the correct answer.

It’s ironic that there are two reasonable ways to approach this problem without using the Law of Cosines, as this was the only problem on this Trigonometry exam that tested the student’s knowledge of this important relationship.