Application Statistics Technology
Statistically Solving Crossword Puzzles
I am lover of crossword puzzles. I do the NYT crossword puzzle regularly, I’ve competed in the American Crossword Puzzle Tournament, and I’ve even dabbled in constructing puzzles myself.
There’s a great deal of crossover between math lovers and crossword puzzle lovers, and one example of this crossover is Matthew Ginsberg. Ginsberg is a regular puzzle constructor, has a PhD in math from Oxford, and is an expert in artificial intelligence.
Not a huge stretch, then, that he has developed a rather effective crossword puzzle solving robot, Dr. Fill, that is now challenging the top human performers .
Ginsberg runs a company that produces software for the Air Force that helps calculate the most efficient flight path for airplanes. Here’s the cool part: “Some of the statistical techniques [used to calculate optimal paths of airplanes] are also handy, it turns out, for solving crossword puzzles.”
Yet another example of how statistical reasoning is emerging as primary tool in modern science and society!
Geometry Teaching
A Waste of Marshmallows
While working on the geometry of the Platonic Solids, we spent some class time constructing them from chopsticks and marshmallows.
We had a lot of fun putting them together!
Unfortunately, the more complicated structures weren’t really strong enough to stand on their own. And after the fact, we realized that we probably shouldn’t leave marshmallows sitting around the classroom indefinitely.
But it certainly was lively way to wrap up a unit on geometric solids! You can see more pictures of the activity on my Facebook page.
Application Appreciation Resources
Mathematics of Juggling
This is an excellent, in-depth video on the mathematics of juggling, from Cornell University professor (and world-class juggler) Allen Knutson.
http://www.youtube.com/watch?v=38rf9FLhl-8
This hour-long video covers the mathematical notation developed to classify and communicate juggling patterns, and Knutson explains how that inherent mathematical structure can be used to create new patterns.
There’s a lot of very sophisticated math here, which may surprise some people. But as Knutson says at the beginning, “Anything that is sufficiently understood … there should be a mathematics of that thing.”
There’s also some good juggling in here, too!
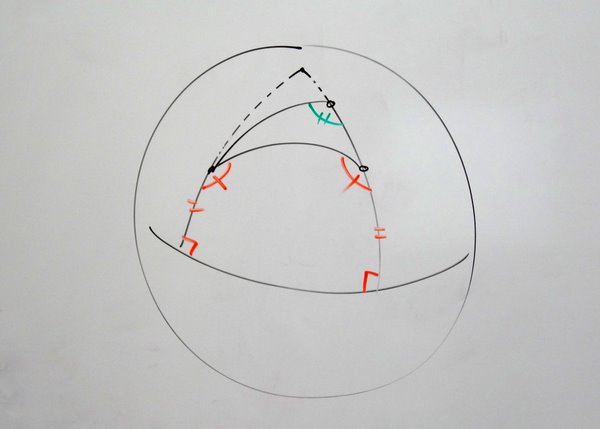
Geometry
The Saccheri Quadrilateral
We’ve been exploring non-Euclidean geometries lately, and the Saccheri Quadrilateral plays a pivotal role in this particular mathematical history.
The Saccheri quadrilateral is a biperpendicular quadrilateral with two congruent legs. It’s an object that is “obviously” a rectangle in Euclidean geometry, but proving that without the aid of the parallel postulate turns out to be rather tricky.
In fact, just proving that the measure of the green angle is less than the measure of the orange angle is pretty tough!