August 2011

Fun With a Favorite Triangle

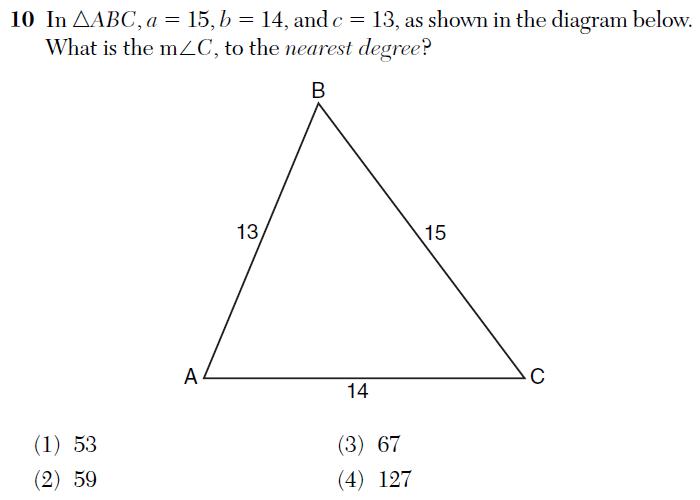
In a post examining the quality of New York State Math Regents exams, I considered the following problem from the 2011 Algebra 2 / Trigonometry exam:

In triangle ABC, we have a = 15, b = 14, and c = 13. Find the measure of angle C.

This problem is designed to test the student’s knowledge of the Law of Cosines. The Law of Cosines is an equation relating the three sides and one angle of the triangle; knowledge of any three of those four quantities allows you to determine the fourth. Substitute the three sides into the equation, perform some algebra and simple trigonometry, and you’ll get the angle.

This isn’t just any triangle, though: this is the famous 13-14-15 triangle. The 13-14-15 triangle has some special properties that allow you to solve this problem without using the Law of Cosines!

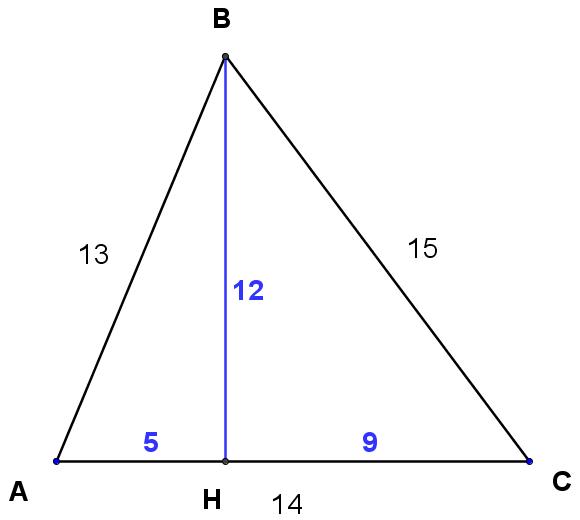
For example, when you drop the altitude the side of length 14, something amazing happens.

Altitudes are perpendicular to bases, so two applications of the Pythagorean Theorem and a little algebra show that the foot of the altitude, H, divides AC into segments of length 5 and 9. This means that triangle AHB is a right triangle with sides 5, 12, and 13 and triangle CHB is a right triangle with sides 9, 12, and 15. As it turns out, our 13-14-15 triangle is just two famous right triangles glued together along a common side!

This makes finding the measure of angle C easy: since C is an angle in a known right triangle, just use right triangle trigonometry! Much easier than using the Law of Cosines.

And for the record, this was a multiple choice question. A clever student had yet another opportunity to eschew the Law of Cosines.

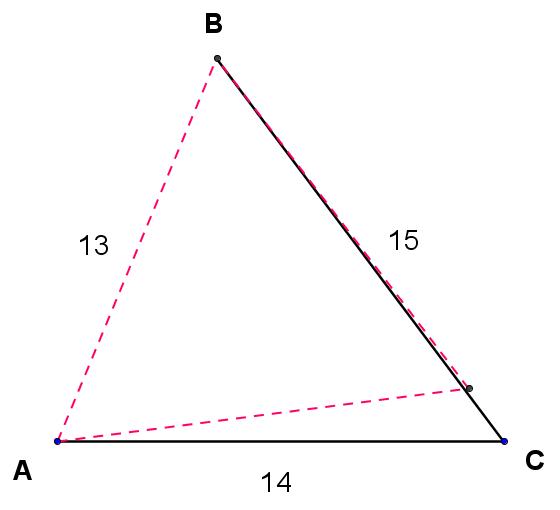
In any triangle, the smallest angle is opposite the shortest side. This allows us to immediately conclude that angle C is less than 60 degrees and thereby eliminate two of the four answer choices, 67 and 127. Similarly, the longest side of a triangle is opposite the largest angle, which means that angle A is greater than 60 degrees. Using a straight-edge and compass, we can construct the following equilateral triangle with side AB.

The two remaining choices for the measure of angle C are 53 and 59. Our diagram suggests that angle B is very close to 60 degrees. Since A is bigger than 60 degrees, C must be less than 60 degrees by roughly that same amount. So the question is now ‘Is the measure of angle A 7 degrees more than 60, or 1 degree more than 60?”. If the diagram is to scale (mine is; I’m not sure about the diagram included in the Regents exam), a 7-degree difference seems more likely. It’s admittedly not a rigorous solution, but it’s not a bad way to navigate to the correct answer.

It’s ironic that there are two reasonable ways to approach this problem without using the Law of Cosines, as this was the only problem on this Trigonometry exam that tested the student’s knowledge of this important relationship.

By patrick honner, 13 years9 years ago

Teaching

Lecturing and Teaching

This article by David Bressoud from the Mathematical Association of America summarizes some interesting research about “lecture-style” teaching.

https://www.maa.org/columns/launchings/launchings_07_11.html

An experiment conducted in an introductory physics course at the University of British Columbia compared students taught by traditional lecture with those taught by a clicker-based peer instruction system. The two groups of students were closely controlled at the beginning of the semester, both receiving lecture-style instruction. Then after 12 weeks, the instructional approach toward one group changed dramatically.

While the control group continued to receive traditional instruction, the experimental group began receiving clicker-based peer instruction. The experienced professor was replaced by two graduate students knowledgeable in physics and trained in this particular instructional methodology, but otherwise lacking in teaching experience. The results were dramatic: by the end of the semester, the average test score of the experimental group was 2.5 standard deviations above the average in the control group.

The peer instruction relied heavily on student-to-student and whole-group discussion of material during class, which is largely credited for the gains in performance. Bressoud has some interesting things to say about what this means for math instruction, inviting us to read more about how to shut up and teach.

By patrick honner, 13 years4 years ago

Teaching

Are These Tests Any Good? Part 3

This is the third entry in a series examining the 2011 NY State Math Regents exams. The basic premise of the series is this: if the tests that students take are ill-conceived, poorly constructed, and erroneous, how can they be used to evaluate teacher and student performance?

In Part 1, I looked at several questions that demonstrated a significant lack of mathematical understanding on the part of the exam writers. In Part 2, I looked at several poorly constructed questions that were vague, incoherent, or tested irrelevant material. Here, in Part 3, I’ll look at a single question that highlights problems with the scope of the exams.

This is number 10 from the 2011 Algebra 2 / Trigonometry Regents exam: given the three sides of a triangle, find the measure of one of the angles.

There is nothing wrong with this question. It’s clear and unambiguous. It connects to a fundamental idea in trigonometry, that knowing three pieces of information is often enough to determine everything about that triangle. And the question is designed to test the student’s knowledge of a fundamental skill in trigonometry: applying the Law of Cosines.

The problem here is that this is only question on this exam related to these topics. This two-point, multiple choice question is the only place on this Trigonometry exam that requires the use of either the Law of Cosines or the Law of Sines.

Perhaps there is a useful discussion to be had about just how important the Laws of Sines and Cosines are. To me, mastery of these theorems is one of the clear end-goals of a trigonometry course. Trigonometry literally means “measure of triangles”, and these two theorems represent the culmination of our knowledge about measuring triangles. Therefore, they should be featured more prominently in a final assessment.

It’s reasonable to debate just how prominently they should be featured, but it’s hard to imagine any trigonometry teacher agreeing that, based on their relative importance, two points out of 88 is a reasonable representation.

Furthermore, a debate about the relative importance of these particular theorems becomes less meaningful when you realize what, instead, appears on this exam. A rough estimate suggests that 12-14 points on this test deal with quadratic functions, a topic from Algebra 1. That’s 15% of the exam. In fact, a review of the entire test suggests that 34-36 of the points relate to topics that should be taught in an introductory Algebra course; that’s nearly 40% of the exam. Why are we testing 9th grade material on an 11/12th grade Regents Exam? That’s probably a topic for another day.

Related Posts

Regents Recaps

By patrick honner, 13 years4 years ago

Statistics Teaching

More Meaningless Education Research

There is no shortage of dubious education research. Reports “proving” that new teachers are better than old, charter schools are better than non-charter schools, and graduate schools of education are useless seem to pop up frequently. If you have a loose-grasp of statistics and the willingness to tell someone what they want to hear, chances are there’s funding available for your study.

So it was no surprise to see exam schools finally make their way into the discourse. The following study appeared in the New York Times, grabbing headlines with its claim that “the impact of attending an exam school school on college enrollment or graduation is, if anything, negative.”

http://artsbeat.blogs.nytimes.com/2011/08/16/thinking-cap-angst-before-high-school/

Exam schools grant admission based on a standardized test. By achieving a minimum score on the test (the school’s “cutoff”), the student can choose to attend the school. These public schools typically offer advanced courses and more rigorous instruction, and one would think that students would get a lot out them. Not according to the authors of this study, who conclude that, in these schools, students’ “actual human capital essentially remains unchanged”. In jargon common to these kinds of studies, exam school schools don’t add any value to the educational experience of students.

A cursory review of the study suggests some obvious problems, many of which are pointed out in the comments section of the original Times article. However, a close review of the study revealed something so absurd, it makes the study seem not so much flawed as intentionally misleading by design.

The basic premise of the study is to compare students who just make the cutoff for an exam school with those who just miss that cutoff. In theory, since these students have similar tests scores, they start with similar levels of ability. Some of them enter the exam school, and some of them don’t. By comparing their later achievement, we can get a sense of what, if anything, attendance at the exam school adds.

Let’s say that Student 1 just makes the cutoff for Exam School A, and Student 2 just misses that cutoff and thus attends a different school. The study claims that Students 1 and 2 will go on to have similar SAT scores and have roughly the same chance of graduating college. That is, attending the exam school does not add any value for Student 1.

What the study doesn’t take into account is that the school Student 2 ends up attending is also likely to be an exam school! Student 2, who just missed the cutoff for Exam School A, might very well attend Exam School B, which has a lower cutoff. In the eyes of this study, however, Student 2’s success at Exam School B counts as evidence that exam schools don’t add value!

In the New York City system, where this study was conducted, this situation arises frequently. A student might miss the cutoff for one exam school but attend another exam school. Indeed, the authors themselves note that in the case of one particular school, 40% of the students who miss the cutoff end up attending a second particular exam school. And when they succeed, they all count as evidence against exam schools.

There are other serious issues regarding this study’s methodology, but to me this is the most significant. Moreover, the obvious gap between what was actually done and what was purported to be done is very disturbing.

I wonder how closely such studies are read, and I wonder what this has to say about the state of current education “research” in general.

By patrick honner, 13 years4 years ago