I’ve presented on Desmos many times to teachers, administrators, and students. So I was excited to bring that experience to the Math for America community through my workshop, An Introduction to Desmos, at the MfA offices in New York City.
Nearly 50 MfA teachers attended, and it was a very active and engaged bunch. Most attendees were familiar with Desmos, and many were using it in their classrooms. But I got the sense that everyone’s eyes were opened a bit wider to the power and possibility of this mathematical technology.
Participants began by working through a document I’ve put together that functions as a guided tour of Desmos. I’ve used this document many times with both teachers and students: it provides a quick overview of the power and breadth of the functionality of Desmos, and it allows me to circulate and answer, and ask, questions. [You can find the document here: Introduction to Desmos]
The second part of the workshop had participants working on a series of content-specific challenges. The goal was to use get teachers using Desmos to build mathematical objects. For example, some teachers worked through these parabola challenges:
Construct an arbitrary parabola
(a) with vertex (2,3)
(b) with vertex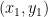 
(c) with roots 2 and 3
(d) with roots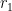 
and 
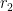
(f) with focus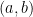 
and directrix 
There were similarly structured challenges for Lines, Transformations, Regions, and several other areas. Participants could choose what to work on based on what they taught or what they were interested in.
As I circulated the room, I answered lots of good questions. And I listened in as teachers talked about how they were already using Desmos in their classrooms. I was especially gratified to hear several teachers tell me that they learned something in the workshop that would have made yesterday’s lesson better. It felt good to deliver immediate impact to my colleagues, and I’m excited to know that many teachers have already integrated Desmos into their instruction.
Throughout the workshop I emphasized that the real power of Desmos is not as a presentation tool, but as a creative tool. I often describe Desmos as a mathematical makerspace: a place where we can design and build using the tools and techniques of mathematics. As teachers, it’s tempting to see Desmos primarily as a tool for demonstrating mathematics to our students, but it’s true power lies in how it can help us all, teachers and students alike, make mathematics.
You can find more of my work with Desmos here. And you can see pictures of the workshop here.
I’m excited to be participating in this summer’s Scratch@MIT conference.
