Technology

This is Jeopardy!

jeopardy boardIn the past we tested the prowess of our supercomputers by teaching them to play chess and pitting them against humanity’s greatest players.  Today we test our supercomputers by filling them up with trivia, arming them with a quick trigger finger, and pitting them against America’s greatest Jeopardy! contestants.

On February 14th, 15th, and 16th, IBM’s Watson will compete against Jeopardy! superstars Ken Jennings and Brad Rutter.

This should be a lot of fun.  I can’t wait to see what Watson’s Daily Double strategy is!

By patrick honner, ago

2010: The Year in Facebook Statistics

facebook logoThis is a cool summary of 2010 in terms of Facebook-related statistics:

http://www.siliconrepublic.com/digital-life/item/19778-facebooks-2010-by-the-numb

With 500 million (!) users, Facebook is rapidly becoming a source of seemingly limitless data about how people live and interact in modern society.  Some of the highlights:

  • Nearly 61 million people changed their relationship status to in a relationship / engaged / married
  • Nearly 43 million people changed their relationship status to single
  • Over 6000 pages were liked every second!  (Speaking of which, how about liking my page?)

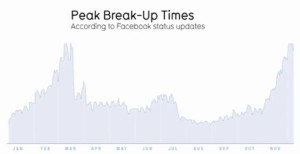
The potential applications of analysis of this data, both good and bad, are mind blowing.  As previously noted, people have used Facebook data to identify peak break-up times and to predict someone’s sexual orientation based on their various connections and activity.

By patrick honner, ago

Math Photo: (Sine) Waves on the Beach

While on vacation, I passed some of my time looking for math on the beach, and I saw a sine wave creeping up the shore.

sine wave in nature

I thought I might be looking too hard for something mathematical, thereby seeing things that weren’t really there.  Thankfully, Geogebra is well-equipped to justify my observations.

wave sine wave equation

Or perhaps it’s more accurate to say that Geogebra helps enable my obsessions.

By patrick honner, ago

Shocking Mathematical Results

 

Welectroshock therapyhen it comes out that I’m a math person, the most common response from people I meet is “I was never very good at math“.  After a lifetime of struggling to find the appropriate response, I finally have something positive and proactive to say:  go get yourself some electroshock therapy.

According to a recent study, running a mild electric current through the brain seems to temporarily increase mathematical ability.   Apparently the study involved teaching the subjects a new numeration system (could it have been octomatics?) and testing their ability to organize those symbols before and after electrical stimulation of the parietal lobe.

In addition to slightly increasing mathematical ability and potentially treating dyscalculia, there is hope that such electrical stimulation could improve other brain function, as well.

Now, how can I bring this revolutionary technique into my classroom?

By patrick honner, ago

Facebook Formulas

peak breakup timesThis graph on the right represents break ups per day, as determined by an analysis of Facebook status changes.  The data suggests that break-ups seem to occur most frequently in mid-February and late November.

Drawing conclusions from data is always dicey, and there are probably a lot of holes to poke in the methodology here, but it certainly is fun trying to attach meaning to these numbers!

This graph was featured in a TED Talk given by David McCandless, who runs the wonderful website www.informationisbeautiful.net.

The whole talk can be found here; this chart comes up at around the 6:50 mark.

The amount of data available through social networking sites is mindblowing, and it can’t be long before it will be used in some significant way.  Indeed, a group of MIT students has already devised a system, cleverly titled Project Gaydar, that, with some accuracy, identifies the sexual orientation of a Facebook user based on friends, likes, and other connections.

What will they compute about us next?

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: