Geometry

3D Street Art

The painter Edgar Mueller uses dilation and perspective tricks to create absolutely mind-blowing three-dimensional pavement art.

http://www.metanamorph.com/

The website is a little clumsy, but there are some really cool projects here, including The Crevasse, The Waterfall, and Lava Burst.  There are also several videos showing how the artist puts these perplexing pavement paintings together.

For an interesting application of this idea, check this out:  a 3D pavement painting of a child playing in the middle of the street!  The idea was to get the attention of speeding drivers.  I bet it did just that!

By patrick honner, ago

Mobius Transformation Video

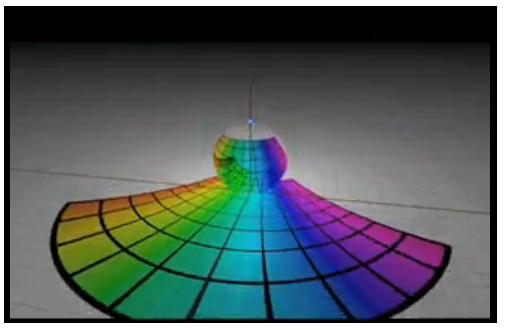
Not only is this visualization of generalized Mobius transformations mesmerizing and beautiful, it is the clearest demonstration of inversion that I have ever seen:

http://www.youtube.com/watch?v=JX3VmDgiFnY

This short movie visually explains all the basic transformations of the plane:  translation, rotation, dilation, and inversion.  Then it demonstrates how all of these transformations of the plane can really be thought of as simple translations and rotations of the sphere!

If I had seen this video a few decades ago, I might not have given up on topology as quickly as I did.

By patrick honner, ago

Folding Steel

This is an amazing application of origami:  a steel grocery bag that can fold flat!

http://news.sciencemag.org/sciencenow/2011/03/paper-plastic-or-steel.html

Although you probably wouldn’t want to carry these to the store with you, this result could have real applications in industrial packaging.  In addition, it’s another step towards the mathematical-origamist’s dream:  designing building that can rearrange and rebuild itself as needed!

A great talk by Erik Demaine on mathematical origami opened my eyes have this amazing application of mathematics, and my students and I have been having a lot of fun with folding ever since!

By patrick honner, ago

Math and Computer Animation

This is a clear, concise, and fascinating overview of how some very advanced mathematical ideas are making their way into 3-D animation.

http://www1.ams.org/samplings/feature-column/fcarc-harmonic

Here’s the basic setup.   In order to efficiently model a character, you approximate it with a frame that is built around a few important points.  To move the character, you focus on moving just those points that define the frame.  Thus, moving the character from point A to point B boils down to understanding where those handful of crucial points go.

The tricky part is figuring out a way to smoothly bring all those in-between points along for the ride, and that’s where the math comes in.  The secret is to think of those in-between points as averages of the points that define the frame.  The article explains how barycentric coordinates, harmonic functions. and a surprising amount of calculus are being used to pull off this movie magic!

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: